题目内容
18．已知抛物线的顶点为（1，-1）且经过原点，则抛物线截x轴的线段长为1．分析 由抛物线的顶点横坐标可知抛物线的对称轴为x=1，又因为抛物线经过原点，进而可求出抛物线和x轴的另外一个交点，进而可求出抛物线截x轴的线段长．
解答 解：
∵抛物线的顶点为（1，-1），
∴抛物线的对称轴为x=1，
∵抛物线经过原点，
∴抛物线和x轴的另外一个交点的坐标为（-1，0），
∴抛物线截x轴的线段长为|-1-0|=1，
故答案为：1．
点评 本题考查了抛物线和x轴交点的问题，求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y=0，即ax2+bx+c=0，解关于x的一元二次方程即可求得交点横坐标．
练习册系列答案
名校课堂系列答案
相关题目
如图，二次函数y=ax2-4ax与x轴交于O，A两点，y轴上有一点B（0，2），作经过O，A，B三点的⊙C，点P是第一象限内⊙C上的任意一点，连接BP，AP，当四边形OAPB面积最大时，点P的坐标为（3，3）．
6．已知函数y=x2-2mx+2016（m为常数）的图象上有三点：A（x1，y1），B（x2，y2），C（x3，y3），其中x1=-$\sqrt{2}$+m，x2=$\frac{2}{3}$+m，x3=m-1，则y1、y2、y3的大小关系是（ ）
| A． | y1＜y3＜y2 | B． | y3＜y1＜y2 | C． | y1＜y2＜y3 | D． | y2＜y3＜y1 |
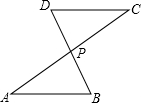如图，AC与BD交于点P，AP=CP，从以下四个论断①∠B=∠D，②BP=DP，③AB=CD，④AB∥CD中选择一个论断作为条件，则不一定能使△APB≌△CPD的论断是③．