题目内容
10.写出一组直角三角形的三边长5,12,13.(要求是勾股数但3、4、5和6、8、10除外)分析 根据勾股数定义:满足a2+b2=c2 的三个正整数,称为勾股数进行解答.
解答 解:52+122=132,因此5,12,13可以构成直角三角形,又都是正整数,因此5,12,13是勾股数,
故答案为:5,12,13.
点评 此题主要考查了勾股数的定义,及勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.

练习册系列答案
相关题目
1.下列各组数为勾股数的是( )
| A. | 7、8、9 | B. | 1、$\sqrt{2}$、$\sqrt{3}$ | C. | 5、12、13 | D. | $\frac{3}{5}$、$\frac{4}{5}$、1 |
2. 如图,已知AB=CD,AE=CF,要证明△ABF≌△CDE,还需添加的已知条件是( )
如图,已知AB=CD,AE=CF,要证明△ABF≌△CDE,还需添加的已知条件是( )
 如图,已知AB=CD,AE=CF,要证明△ABF≌△CDE,还需添加的已知条件是( )
如图,已知AB=CD,AE=CF,要证明△ABF≌△CDE,还需添加的已知条件是( )| A. | ∠B=∠D | B. | BF∥DE | C. | BF=DE | D. | AF=CE |
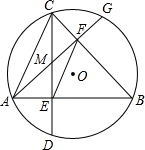 如图,在⊙O中,弦AB⊥弦CD于E,弦AG⊥弦BC于F点,CD与AG相交于M点.
如图,在⊙O中,弦AB⊥弦CD于E,弦AG⊥弦BC于F点,CD与AG相交于M点.