题目内容
7.下列分式运算,正确的是( )| A. | ($\frac{3x}{5y}$)2=$\frac{3{x}^{2}}{5{y}^{2}}$ | B. | $\frac{1}{x-y}-\frac{1}{y-x}$=0 | C. | $\frac{1}{3x}+\frac{1}{3y}=\frac{1}{3(x+y)}$ | D. | ($\frac{{x}^{2}}{-y}$)3=-$\frac{{x}^{6}}{{y}^{3}}$ |
分析 根据各个选项中的式子,可以计算出正确的结果,从而可以判断哪个选项是正确的.
解答 解:∵$(\frac{3x}{5y})^{2}=\frac{9{x}^{2}}{25{y}^{2}}$,故选项A错误,
∵$\frac{1}{x-y}-\frac{1}{y-x}=\frac{1}{x-y}+\frac{1}{x-y}=\frac{2}{x-y}$,故选项B错误,
∵$\frac{1}{3x}+\frac{1}{3y}=\frac{y+x}{3xy}$,故选项C错误,
∵$(\frac{{x}^{2}}{-y})^{3}=-\frac{{x}^{6}}{{y}^{3}}$,故选项D正确,
故选D.
点评 本题考查分式的混合运算,解答本题的关键是明确分式混合运算的计算方法.

练习册系列答案
相关题目
15.下列结论正确的是( )
| A. | 不相交的两条直线叫做平行线 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 垂直于同一条直线的两条直线互相平行 | |
| D. | 平行于同一条直线的两条直线互相平行 |
2.袋子中装有15个黑球、1个白球,它们除颜色外无其他差别,随机从袋子中摸出一个球,则下列说法正确的是( )
| A. | 这个球可能是白球 | |
| B. | 摸到黑球、白球的可能性的大小一样 | |
| C. | 这个球一定是黑球 | |
| D. | 事先能确定摸到什么颜色的球 |
19.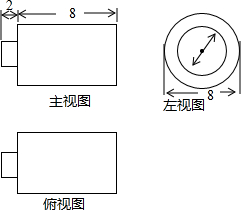 如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
 如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )
如图,是某几何体的三视图,根据图中所标的数据求得该几何体的体积为( )| A. | 120π | B. | 132π | C. | 136π | D. | 236π |
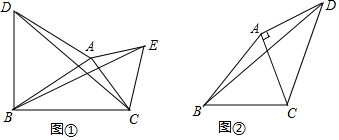
 如图,已知AD⊥BC,EF⊥BC,∠4=∠C,试证明∠1=∠2.
如图,已知AD⊥BC,EF⊥BC,∠4=∠C,试证明∠1=∠2.