题目内容
16.阅读理解:将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$,我们把$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$称作二阶行列式,规定它的运算法则为$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.如$|\begin{array}{l}{1}&{2}\\{3}&{4}\end{array}|$=1×4-2×3=-2.
(1)计算:$|\begin{array}{l}{2a^2}&{a^3}\\{a}&{3a^2}\end{array}|$
(2)若$|\begin{array}{l}{x+2}&{x+3}\\{x-1}&{x+2}\end{array}|$=3,求x的值.
分析 根据定义即可化简运算求出答案.
解答 解:(1)原式=2a3•3a2-a3•a
=6a4-a4
=5 a4
(2)(x+2)2-(x+3)(x-1)=3
x2+4x+4-(x2+2x-3)=3
2x+7=3
2x=-4
x=-2
点评 本题考查学生理解能力,解题的关键是正确理解二阶行列式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
7.下列分式运算,正确的是( )
| A. | ($\frac{3x}{5y}$)2=$\frac{3{x}^{2}}{5{y}^{2}}$ | B. | $\frac{1}{x-y}-\frac{1}{y-x}$=0 | C. | $\frac{1}{3x}+\frac{1}{3y}=\frac{1}{3(x+y)}$ | D. | ($\frac{{x}^{2}}{-y}$)3=-$\frac{{x}^{6}}{{y}^{3}}$ |
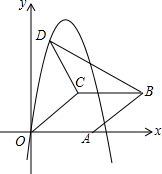 如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-(x-3)2+9上一点,且在x轴上方,则△BCD面积的最大值为15.
如图,在平面直角坐标系中,菱形OABC的顶点A在x轴正半轴上,顶点C的坐标为(4,3),D是抛物线y=-(x-3)2+9上一点,且在x轴上方,则△BCD面积的最大值为15.