题目内容
12.【探究】如图①,分别以△ABC的两边AB和AC为边向△ABC外作正三角形ABD和正三角形ACE,连结DC、BE,求证:DC=BE.【拓展】如图②,在四边形ABCD中,AB=BC=5,∠ABC=45°,连结AC、BD,若∠DAC=90°,AC=AD,则BD的长为5$\sqrt{3}$.
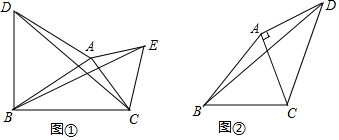
分析 【探究】根据等边三角形的性质得出AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS推出△DAC≌△BAE即可;
【拓展】根据全等三角形的性质得到CE=BD,由勾股定理即可得到结论.
解答 解:【探究】∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△DAC≌△BAE(SAS),
∴CD=BE;
【拓展】如图②,以AB为边向外作等腰直角三角形AB,AE=AB,∠BAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,$\left\{\begin{array}{l}{AE=AB}\\{∠CAE=∠BAD}\\{AC=AD}\end{array}\right.$,
∴△ACE≌△ABD,
∴CE=BD,
∵BE=$\sqrt{2}$AB=5$\sqrt{2}$,
∵∠ABC=45°,
∴∠EBC=90°,
∴CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=5$\sqrt{3}$,
∴BD=5$\sqrt{3}$,
故答案为:5$\sqrt{3}$.
点评 本题考查了等边三角形的性质,等腰直角三角形的性质,全等三角形的性质和判定的应用,勾股定理,关键是求出△DAC≌△BAE,题目是一道比较好的题目,难度适中.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
2.下列图形中,∠1和∠2是内错角的是( )
| A. | 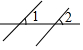 | B. | 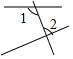 | C. | 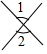 | D. | 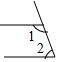 |
3.下列图形是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.下列分式运算,正确的是( )
| A. | ($\frac{3x}{5y}$)2=$\frac{3{x}^{2}}{5{y}^{2}}$ | B. | $\frac{1}{x-y}-\frac{1}{y-x}$=0 | C. | $\frac{1}{3x}+\frac{1}{3y}=\frac{1}{3(x+y)}$ | D. | ($\frac{{x}^{2}}{-y}$)3=-$\frac{{x}^{6}}{{y}^{3}}$ |
 如图,⊙O是等边△ABC的外接圆,M是BC延长线上一点,连接AM交⊙O于点D,延长BD至点N,使得BN=AM,连接CN,MN.
如图,⊙O是等边△ABC的外接圆,M是BC延长线上一点,连接AM交⊙O于点D,延长BD至点N,使得BN=AM,连接CN,MN.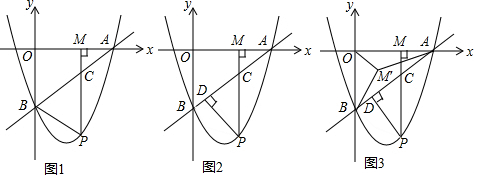
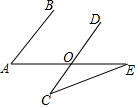 如图,AB∥CD,∠C=35°,∠E=25°,则∠A=60°°.
如图,AB∥CD,∠C=35°,∠E=25°,则∠A=60°°.