��Ŀ����
6�� ��ͼ����֪���κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�P������ΪC��3��-16����
��ͼ����֪���κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�P������ΪC��3��-16������1����˺����Ĺ�ϵʽ��
��2������C����x��ĶԳƵ�D��˳������A��C��B��D�������������ϴ��ڵ�E��ʹֱ��PE���ı���ABCD�ֳ������ȵ������ı��Σ����E�����ꣻ
��3���ڣ�2���������£�ֱ��PE���ڶ��κ���y=x2+bx+c��ֵ��x��ȡֵ��Χ��
��4��FΪ�������ϵ�һ�����㣬�ǡ�ABF�����ΪS����S=16�������Ӧ��F������꣮
���� ��1��ֱ�����ö���ʽ������κ�������ʽ���ɣ�
��2���������ε����ʵó�ֱ��PE�ع�����ACBD�ĶԳ�����M���������ֱ��PE�Ľ���ʽ����������������������𰸣�
��3�����ã�2���������Ϻ���ͼ��ó��𰸣�
��4��������֪�ó�F�������꣬�������F�����꣮
��� �⣺��1���߶��κ���y=x2+bx+c�Ķ���ΪC��3��-16����
����κ�������ʽΪ��y=��x-3��2-16=x2-6x-7��
��2����ͼ1����ֱ��PE��Ӧ�ĺ�����ϵʽΪ��y=kx+b��������ɵã��ı���ACBD�����Σ�
��ֱ��PE�ع�����ACBD�ĶԳ�����M��
��P��0��-7����M��3��0��������y=kx+b�ã�
$\left\{\begin{array}{l}{b=-7}\\{3k+b=\frac{7}{3}}\end{array}\right.$��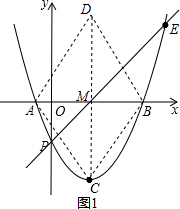
��ã�$\left\{\begin{array}{l}{k=\frac{7}{3}}\\{b=-7}\end{array}\right.$��
��ֱ��PE�Ľ���ʽΪ��y=$\frac{7}{3}$x-7��
�Ӷ����������飺$\left\{\begin{array}{l}{y=\frac{7}{3}x-7}\\{y={x}^{2}-6x-7}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=\frac{25}{3}}\\{y=\frac{112}{9}}\end{array}\right.$��
��������ɵã���E��$\frac{25}{3}$��$\frac{112}{9}$����
��3���۲�ͼ��ã�0��x��$\frac{25}{3}$ʱֱ��PE���ڶ��κ���y=x2+bx+c��ֵ��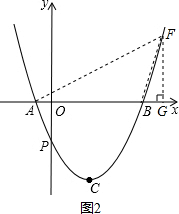
��4����ͼ2��������������ĵ�F������F��x��y��������F��FG��x�ᣬ����Ϊ��G����������AB=8��
��S=$\frac{1}{2}$��|y|��8=16��
��ã�y=��4��
��y=4ʱ��x2-6x-7=4��
��ã�x=3��2$\sqrt{5}$��
��y=-4ʱ��x2-6x-7=-4��
��ã�x=3��2$\sqrt{3}$��
��F1��3+2$\sqrt{5}$��4����F2��3-2$\sqrt{5}$��4����F3��3+2$\sqrt{3}$��-4����F4��3-2$\sqrt{3}$��-4����
���� ������Ҫ�����˶���ʽ����κ�������ʽ�Լ�����������һԪ���η��̵Ľⷨ��֪ʶ��ע�����ν�ϵ�Ӧ�ã���������ó�F���������ǽ���ؼ���

 ����˼ά�żӿ���ϵ�д�
����˼ά�żӿ���ϵ�д� �����Ծ�ϵ�д�
�����Ծ�ϵ�д�| A�� | ��С | B�� | ���� | C�� | ��� | D�� | ��ȷ�� |
 ��ͼ���ھ���ABCD�У�E�DZ�AB�ϵĵ㣬���߶�BE��B��˳ʱ����תһ���ǶȺ�CD�ڵ�F����ʱAE=CF������EF���Խ���AC�ڵ�O����BE=BF����BEF=2��BAC��FC=2����AB�ij�Ϊ��������
��ͼ���ھ���ABCD�У�E�DZ�AB�ϵĵ㣬���߶�BE��B��˳ʱ����תһ���ǶȺ�CD�ڵ�F����ʱAE=CF������EF���Խ���AC�ڵ�O����BE=BF����BEF=2��BAC��FC=2����AB�ij�Ϊ��������| A�� | 8$\sqrt{3}$ | B�� | 6 | C�� | 4$\sqrt{3}$ | D�� | 8 |
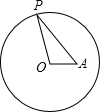 ��ͼ����A�ڰ뾶Ϊ3�ġ�O�ڣ�OA=$\sqrt{3}$��PΪ��O��һ�㣬����OPAȡ���ֵʱ��PA�ij�����$\sqrt{6}$��
��ͼ����A�ڰ뾶Ϊ3�ġ�O�ڣ�OA=$\sqrt{3}$��PΪ��O��һ�㣬����OPAȡ���ֵʱ��PA�ij�����$\sqrt{6}$�� ��ͼ����֪��A��2��m����B��n��1����������y=x2��ͼ����
��ͼ����֪��A��2��m����B��n��1����������y=x2��ͼ���� ��ͼ����A��O��D������һ��ֱ���ϣ���AOB=20�㣬��BOC=3��COD��
��ͼ����A��O��D������һ��ֱ���ϣ���AOB=20�㣬��BOC=3��COD��