题目内容
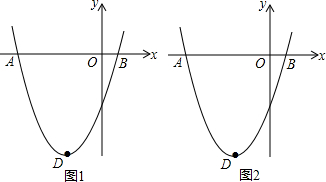
11. 如图,已知点A(2,m),B(n,1)在抛物线y=x2的图象上
如图,已知点A(2,m),B(n,1)在抛物线y=x2的图象上(1)求m、n的值;
(2)在y轴上找一点P,使得P到A、B两点的距离之和最短,求出此时P点坐标.
分析 (1)把A(2,m),B(n,1)代入y=x2即可求得m、n的值;
(2)作B点关于y轴的对称点B′(-1,1),连接AB′,进而求出直线AB′的解析式,令x=0,即可得出P点的坐标.
解答 解:(1)把A(2,m),B(n,1)代入y=x2得,
m=22=4,1=n2,
∴n=±1,
∵B在第一象限,
∴n=1;
∴m=4,n=1;
(2)作B点关于y轴的对称点B′(-1,1),连接AB′,
设直线AB′的解析式为y=kx+b,
代入A、B′的坐标得,$\left\{\begin{array}{l}{4=2k+b}\\{1=-k+b}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴y=x+2,
令x=0,则y=2,
∴P(0,2).
点评 此题主要考查了二次函数图象上点的坐标特征以及待定系数法求一次函数解析式,求出一次函数解析式从而得出P点的坐标是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点P,顶点为C(3,-16).
如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点P,顶点为C(3,-16).
 如图,AB∥CD,且AO=CO.求证:AB=CD.
如图,AB∥CD,且AO=CO.求证:AB=CD. 如图,A,B,C,D是直线l上的四个点,M,N分别是AB,CD的中点.
如图,A,B,C,D是直线l上的四个点,M,N分别是AB,CD的中点.