题目内容
8.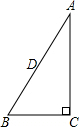 在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.
在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.
分析 要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系,根据直角三角形的性质得到斜边AB的长,再根据直角三角形斜边上的中线等于斜边的一半得出CD的长,然后根据点到圆心距离与半径的关系即可确定该点与圆的位置关系.
解答 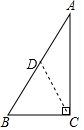 解:连接CD,
解:连接CD,
∵∠C=90°,∠A=30°,
∴BC=$\frac{1}{2}$AB,
∵点D是斜边AB的中点,
∴CD=$\frac{1}{2}$AB,
∴BC=CD,
∴点D在⊙C上.
故答案为:点D在⊙C上
点评 本题根据点到圆心的距离和圆的半径之间的数量关系,来判断点和圆的位置关系.点与圆的位置关系有3种.设⊙O的半径为r,点D到圆心的距离OD=d,则有:
①点D在圆外?d>r;②点D在圆上?d=r;③点P在圆内?d<r.

练习册系列答案
相关题目
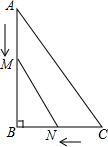 如图,在Rt△ABC中∠B=90°,AB=8m,BC=6m,点M、点N分别从A、C两点同时出发,分别沿AB、CB方向向点B匀速移动,它们的速度都是2m/s,问几秒后,△MBN的面积为Rt△ABC的面积的$\frac{1}{6}$?
如图,在Rt△ABC中∠B=90°,AB=8m,BC=6m,点M、点N分别从A、C两点同时出发,分别沿AB、CB方向向点B匀速移动,它们的速度都是2m/s,问几秒后,△MBN的面积为Rt△ABC的面积的$\frac{1}{6}$? 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连结AD.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连结AD.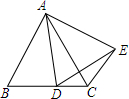 如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE, 如图,直线AD为△ABC的对称轴,BC=6,AD=4,则图中阴影部分的面积为6.
如图,直线AD为△ABC的对称轴,BC=6,AD=4,则图中阴影部分的面积为6.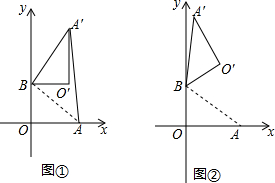 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为ɑ.
在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为ɑ.