题目内容
18.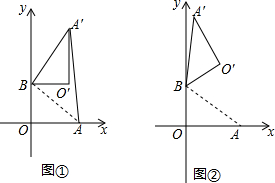 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为ɑ.
在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为ɑ.(1)如图1,若ɑ=90°,求AA′的长;
(2)如图2,若ɑ=120°,求点O′的坐标.
分析 (1)根据勾股定理得AB=5,由旋转性质可得∠A′BA=90°,A′B=AB=5.继而得出AA′=5$\sqrt{2}$;
(2)O′C⊥y轴,由旋转是性质可得:∠O′BO=120°,O′B=OB=3,在Rt△O′CB中,由∠O′BC=60°得BC、O′C的长,继而得出答案.
解答 解:(1)∵点A(4,0),点B(0,3),
∴OA=4,OB=3.
在Rt△ABO中,由勾股定理得AB=5.
根据题意,△A′BO′是△ABO绕点B逆时针旋转900得到的,
由旋转是性质可得:∠A′BA=90°,A′B=AB=5,
∴AA′=5$\sqrt{2}$.
(2)如图,根据题意,由旋转是性质可得:∠O′BO=120°,O′B=OB=3
过点O′作O′C⊥y轴,垂足为C,
则∠O′CB=90°.
在Rt△O′CB中,由∠O′BC=60°,∠BO′C=30°.
∴BC=$\frac{1}{2}$O′B=$\frac{3}{2}$.
由勾股定理O′C=$\frac{3\sqrt{3}}{2}$,
∴OC=OB+BC=$\frac{9}{2}$.
∴点O′的坐标为($\frac{3\sqrt{3}}{2}$,$\frac{9}{2}$).
点评 本题主要考查旋转的性质及勾股定理,熟练掌握旋转的性质是解题的关键.

练习册系列答案
相关题目
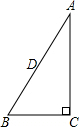 在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.
在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.