题目内容
13. 如图,直线AD为△ABC的对称轴,BC=6,AD=4,则图中阴影部分的面积为6.
如图,直线AD为△ABC的对称轴,BC=6,AD=4,则图中阴影部分的面积为6.
分析 由在△ABC中,AD⊥BC于D点,BD=CD,可得△ABC是等腰三角形,易证得△ABE≌△ACE,△BDF≌△CDF,继而可得S阴影=$\frac{1}{2}$S△ABC,则可求得答案.
解答 解:∵在△ABC中,AD⊥BC,BD=CD,
∴AB=AC,∠ADB=∠ADC=90°,S△ABD=S△ACD,
∴∠BAD=∠CAD,
在△ABE和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAE}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△ACE(SAS),
∴S△ABE=S△ACE,
在△BDF和△CDF中,
$\left\{\begin{array}{l}{BD=CD}\\{∠BDF=∠CDF}\\{DF=DF}\end{array}\right.$,
∴△BDF≌△CDF(SAS),
∴S△BDF=S△CDF,
∴S△BEF=S△CEF,
∵S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×4×6=12,
∴S阴影=$\frac{1}{2}$S△ABC=6.
故答案为:6.
点评 此题考查了等腰三角形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,在直角三角形ACB中,∠C=90°,AC=BC=10cm,点P从A点出发,沿AC以1cm/s的速度向点C运动,同时点Q从B点出发,沿BC以1cm/s的速度向点C运动,则几秒后四边形APQB的面积为32cm2?
如图,在直角三角形ACB中,∠C=90°,AC=BC=10cm,点P从A点出发,沿AC以1cm/s的速度向点C运动,同时点Q从B点出发,沿BC以1cm/s的速度向点C运动,则几秒后四边形APQB的面积为32cm2?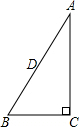 在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.
在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上. 如图,矩形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x<0)的图象上,顶点B、C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是4,则k的值为-8.
如图,矩形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x<0)的图象上,顶点B、C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是4,则k的值为-8.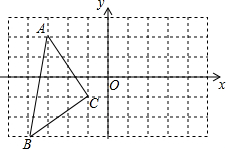 如图,△ABC在平面直角坐标系中的位置如图所示.
如图,△ABC在平面直角坐标系中的位置如图所示.