题目内容
18.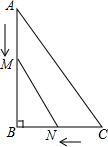 如图,在Rt△ABC中∠B=90°,AB=8m,BC=6m,点M、点N分别从A、C两点同时出发,分别沿AB、CB方向向点B匀速移动,它们的速度都是2m/s,问几秒后,△MBN的面积为Rt△ABC的面积的$\frac{1}{6}$?
如图,在Rt△ABC中∠B=90°,AB=8m,BC=6m,点M、点N分别从A、C两点同时出发,分别沿AB、CB方向向点B匀速移动,它们的速度都是2m/s,问几秒后,△MBN的面积为Rt△ABC的面积的$\frac{1}{6}$?
分析 可设x秒后,S△MBN=$\frac{1}{6}$S△ABC,而此时AM=CN=xm,BM=(8-2x)m,BN=(6-2x)m,S△MBN=$\frac{1}{2}$×BM×BN,S△ABC=$\frac{1}{2}$×8×6,进而可列出方程,求出答案.
解答 解:设x秒后,S△MBN=$\frac{1}{6}$S△ABC,
由题意得(8-2x)×(6-2x)×$\frac{1}{2}$=$\frac{1}{6}$×$\frac{1}{2}$×6×8,
即x2-7x+10=0,
解之,得x1=2,x2=5,
∵BC=6米,
∴0≤x≤6,
∴x1=5不合题意,舍去,
答:当2秒后,S△MBN=$\frac{1}{6}$S△ABC.
点评 此题考查了一元二次方程的应用,这类题目体现了数形结合的思想,通常这类问题可转化为一元二次方程求解,但应注意考虑解的合理性,即考虑解的取舍.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A($\sqrt{3}$,n),过点A作AB⊥x轴于点B,△AOB的面积为$\sqrt{3}$.
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A($\sqrt{3}$,n),过点A作AB⊥x轴于点B,△AOB的面积为$\sqrt{3}$.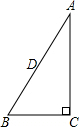 在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.
在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.