题目内容
3.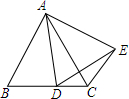 如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,
如图,等边△ABC的边长为2,点D是射线BC上的一个动点,以AD为边向右作等边△ADE,连结CE,(1)求证:△ABD≌△ACE;
(2)若CE=$\frac{1}{2}$,求△ACD的面积;
(3)若△ACE是直角三角形,则BD的长是1或4(直接写出答案).
分析 (1)构建两边及其夹角对应相等的两个三角形全等即可证明.
(2)如图2中,作AM⊥BC于M.由(1)可知BD=CE=$\frac{1}{2}$,求出CD、AM即可解决问题.
(3)分两种情形①如图3中,当∠AEC=90°时,②如图4中,当∠CAE=90°时,分别求解即可.
解答 (1)证明:如图1中,
∵△ABC,△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE.
(2)解:如图2中,作AM⊥BC于M.
∵△ABD≌△ACE,
∴BD=CE=,$\frac{1}{2}$,∵AB=BC=2,
∴CD=BC-BD=$\frac{3}{2}$,
在Rt△ABM中,∵∠AMB=90°,∠BAM=30°,AB=2,
∴AM=AB•cos30°=$\sqrt{3}$,
∴S△ACD=$\frac{1}{2}$•CD•AM=$\frac{1}{2}$×$\frac{3}{2}$×$\sqrt{3}$=$\frac{3\sqrt{3}}{4}$.
(3)解:如图3中,当∠AEC=90°时,
∵△ABD≌△ACE,
∴∠B=∠ACE=60°,
∴∠CAE=90°-∠ACE=30°,
∴EC=BD=$\frac{1}{2}$AC=1.
如图4中,当∠CAE=90°时,
∵△ABD≌△ACE,
∴∠B=∠ACE=60°,BD=CE,
∴∠CEA=90°-∠ACE=30°,
∴EC=2AC=4,
∴BD=CE=4.
综上所述,BD=1或4时,△ACE是直角三角形.
故答案为1或4.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、直角三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会用分类讨论的思想思考问题,属于中考常考题型.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 已知:如图,矩形OABC,OA=6,AB=4,D是BC的中点.动点P从O 点出发,以每秒1个单位的速度,沿着OA、AB、BD运动.设P点运动的时间为t秒.
已知:如图,矩形OABC,OA=6,AB=4,D是BC的中点.动点P从O 点出发,以每秒1个单位的速度,沿着OA、AB、BD运动.设P点运动的时间为t秒. 如图,反比例函数y=$\frac{6}{x}$的图象与一次函数y=kx+b的图象相交于两点A(m,3)和 B(-3,n).
如图,反比例函数y=$\frac{6}{x}$的图象与一次函数y=kx+b的图象相交于两点A(m,3)和 B(-3,n).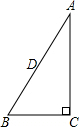 在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.
在Rt△ABC中,∠C=90°,∠A=30°,以点C为圆心,CB为半径画圆,则斜边AB的中点D与⊙C的位置关系是点D在⊙C上.