题目内容
5.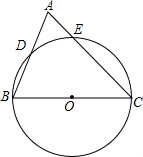 如图所示,△ABC中,BC=4,以BC为直径的半圆交AB于点D,交AC于点E,BD=2,CE=2$\sqrt{2}$.
如图所示,△ABC中,BC=4,以BC为直径的半圆交AB于点D,交AC于点E,BD=2,CE=2$\sqrt{2}$.(1)求∠ABC的度数;
(2)求∠A的度数.
分析 (1)连接CD,根据圆周角定理和直角三角形的性质得到∠BCD=30°,根据直角三角形两锐角互余计算即可;
(2)连接BE,求出∠BCE=45°,根据三角形内角和定理得到答案.
解答 解: (1)连接CD,
(1)连接CD,
∵BC为半圆的直径,
∴∠BDC=90°,又BC=4,BD=2,
∴∠BCD=30°,
∴∠ABC=60°;
(2)连接BE,
∵∠BDC=90°,又BC=4,CE=2$\sqrt{2}$,
∴∠BCE=45°,
∴∠A=180°-∠ABC-∠A=75°.
点评 本题考查的是圆周角定理和直角三角形的性质,掌握直径所对的圆周角是直角是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
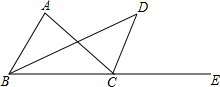 如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;
如图所示,已知BD为△ABC的角平分线,CD为△ABC外角∠ACE的平分线,且与BD交于点D;