��Ŀ����
15����ͼ����MAN=60�㣬APƽ�֡�MAN����B������AP��һ���㣬��C��ֱ��AN���˶�������BC������ABC��0�㣼��ABC��120�㣩����������BC��BA�ֱ��Ƶ�B˳ʱ����ת120�㣬��ת��ǵ����߷ֱ�������AM���ڵ�D�͵�E��
��1����ͼ1������C������AN��ʱ��
�����ж��߶�BC��BD��������ϵ��ֱ��д�����ۣ�
����̽���߶�AC��AD��BE֮���������ϵ��д�����۲�֤����
��2����ͼ2������C������AN�ķ����ӳ�����ʱ��BC������AM�ڵ�F����AB=4��AC=$\sqrt{3}$����ֱ��д���߶�AD��DF�ij���
���� ��1���ٽ��ۣ�BC=BD��ֻҪ֤����BGD�ա�BHC���ɣ��ڽ��ۣ�AD+AC=$\sqrt{3}$BE��ֻҪ֤��AD+AC=2AG=2EG����֤��EB=$\frac{\sqrt{3}}{2}$BE���ɽ�����⣻
��2����ͼ2�У���BG��AM��G��BH��AN��H��AK��CF��K���ɣ�1����֪����ABG�ա�ABH����BGD�ա�BHC����֪BH=GB=2��AH=AG=EG=2$\sqrt{3}$��BC=BD=$\sqrt{B{H}^{2}+C{H}^{2}}$=$\sqrt{31}$��CH=DG=3$\sqrt{3}$���Ƴ�AD=5$\sqrt{3}$����sin��ACH=$\frac{AK}{AC}$=$\frac{BH}{BC}$���Ƴ�$\frac{AK}{\sqrt{3}}$=$\frac{2}{\sqrt{31}}$���ɵ�AK=$\frac{2\sqrt{3}}{\sqrt{31}}$����FG=y����AF=2$\sqrt{3}$-y��BF=$\sqrt{4+{y}^{2}}$���ɡ�AFK�ס�BFG���ɵ�$\frac{AF}{BF}$=$\frac{AK}{BG}$���ɵ÷���$\frac{2\sqrt{3}-y}{\sqrt{4+{y}^{2}}}$=$\frac{\frac{2\sqrt{3}}{\sqrt{31}}}{2}$�����y���ɽ�����⣮
��� �⣺��1���ٽ��ۣ�BC=BD��
���ɣ���ͼ1�У���BG��AM��G��BH��AN��H��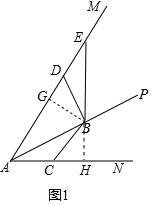
�ߡ�MAN=60�㣬PAƽ�֡�MAN��BG��AM��G��BH��AN��H
��BG=BH����GBH=��CBD=120�㣬
���CBH=��GBD���ߡ�BGD=��BHC=90�㣬
���BGD�ա�BHC��
��BD=BC��
�ڽ��ۣ�AD+AC=$\sqrt{3}$BE��
�ߡ�ABE=120�㣬��BAE=30�㣬
���BEA=��BAE=30�㣬
��BA=BE����BG��AE��
��AG=GE��EG=BE•cos30��=$\frac{\sqrt{3}}{2}$BE��
�ߡ�BGD�ա�BHC��
��DG=CH��
��AB=AB��BG=BH��
��Rt��ABG��Rt��ABH��
��AG=AH��
��AD+AC=AG+DG+AH-CH=2AG=$\sqrt{3}$BE��
��AD+AC=$\sqrt{3}$BE��
��2����ͼ2�У���BG��AM��G��BH��AN��H��AK��CF��K��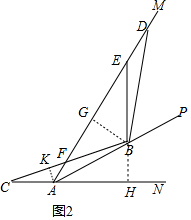
�ɣ�1����֪����ABG�ա�ABH����BGD�ա�BHC��
��֪BH=GB=2��AH=AG=EG=2$\sqrt{3}$��BC=BD=$\sqrt{B{H}^{2}+C{H}^{2}}$=$\sqrt{31}$��CH=DG=3$\sqrt{3}$��
��AD=5$\sqrt{3}$��
��sin��ACH=$\frac{AK}{AC}$=$\frac{BH}{BC}$��
��$\frac{AK}{\sqrt{3}}$=$\frac{2}{\sqrt{31}}$��
��AK=$\frac{2\sqrt{3}}{\sqrt{31}}$����FG=y����AF=2$\sqrt{3}$-y��BF=$\sqrt{4+{y}^{2}}$��
�ߡ�AFK=��BFG����AKF=��BGF=90�㣬
���AFK�ס�BFG��
��$\frac{AF}{BF}$=$\frac{AK}{BG}$��
��$\frac{2\sqrt{3}-y}{\sqrt{4+{y}^{2}}}$=$\frac{\frac{2\sqrt{3}}{\sqrt{31}}}{2}$��
���y=$\frac{10\sqrt{3}}{7}$��3$\sqrt{10}$����������
��DF=GF+DG=$\frac{10\sqrt{3}}{7}$+3$\sqrt{3}$=$\frac{31\sqrt{3}}{7}$��
���� ���⿼�鼸�α任�ۺ��⡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ�������Ǻ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬����Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬�����п�ѹ���⣮

 �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�| A�� | $\sqrt{13}$ | B�� | -$\sqrt{13}$ | C�� | 3$\sqrt{13}$ | D�� | -3$\sqrt{13}$ |
 ������һ�����⣺̽������y=$\frac{1}{x}$+1��ͼ�������ʣ�
������һ�����⣺̽������y=$\frac{1}{x}$+1��ͼ�������ʣ�С������ѧϰһ�κ����ľ��飬�Ժ���y=$\frac{1}{x}$+1��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y=$\frac{1}{x}$+1���Ա���x��ȡֵ��Χ��x��0��
��2���±���y��x�ļ����Ӧֵ��
| x | �� | -4 | -3 | -2 | -1 | -m | m | 1 | 2 | 3 | 4 | �� |
| y | �� | $\frac{3}{4}$ | $\frac{2}{3}$ | $\frac{1}{2}$ | 0 | -1 | 3 | 2 | $\frac{3}{2}$ | $\frac{4}{3}$ | $\frac{5}{4}$ | �� |
��3����ͼ����ƽ��ֱ������ϵxOy�У�������Ա��и��Զ�ӦֵΪ����ĵ㣮��������ĵ㣬�����ú�����ͼ��
��4��д���ú�����һ�����ʸú���û�����ֵ�� �ú���û����Сֵ��
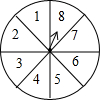 ��ͼ��ת�̱�ƽ���ֳ�8������ÿ������ֱ��ע����1��2��3��4��5��6��7��8������ת��ת��һ�Σ��涨�����ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��һ���������ֵ�����Ϊֹ��д�������¼������ĸ��ʣ�
��ͼ��ת�̱�ƽ���ֳ�8������ÿ������ֱ��ע����1��2��3��4��5��6��7��8������ת��ת��һ�Σ��涨�����ָ��ǡ��ָ�ڷָ����ϣ���ô��תһ�Σ�ֱ��ָ��ָ��һ���������ֵ�����Ϊֹ��д�������¼������ĸ��ʣ�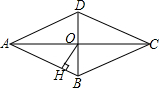 ��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����AC=8��BD=6������O��OH�AAB������ΪH�������ε����Ϊ24����O����AB�ľ���OH=2.4��
��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����AC=8��BD=6������O��OH�AAB������ΪH�������ε����Ϊ24����O����AB�ľ���OH=2.4��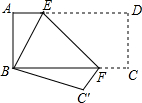 ��ͼ����������ֽƬABCD�۵���ʹ��D���B�غϣ���C����C�䴦���ۺ�ΪEF����AB=1��BC=2����BC��F���ܳ���3��
��ͼ����������ֽƬABCD�۵���ʹ��D���B�غϣ���C����C�䴦���ۺ�ΪEF����AB=1��BC=2����BC��F���ܳ���3��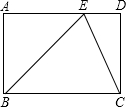 ��ͼ���ھ���ABCD�У���ABC��ƽ���߽�AD�ڵ�E������CE����BC=7��AE=4����CE=5��
��ͼ���ھ���ABCD�У���ABC��ƽ���߽�AD�ڵ�E������CE����BC=7��AE=4����CE=5��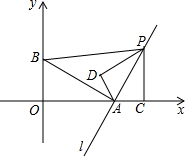 ��ͼ����ֱ������ϵ�У���A��2��0������B��0��1��������A��ֱ��l��ֱ���߶�AB����P��ֱ��l��һ���㣬����P��PC��x�ᣬ����ΪC���ѡ�ACP��AP����180�㣬ʹ��C���ڵ�D��������A��D��PΪ��������������ABP���ƣ�����������������ĵ�P������ΪP��5��2����p��8��8����P��0��-8����P��3��-2����
��ͼ����ֱ������ϵ�У���A��2��0������B��0��1��������A��ֱ��l��ֱ���߶�AB����P��ֱ��l��һ���㣬����P��PC��x�ᣬ����ΪC���ѡ�ACP��AP����180�㣬ʹ��C���ڵ�D��������A��D��PΪ��������������ABP���ƣ�����������������ĵ�P������ΪP��5��2����p��8��8����P��0��-8����P��3��-2����