题目内容
9.解方程组:$\left\{\begin{array}{l}x-2y+4z=12\\ 3x+2y+z=1\\ 4x-z=7\end{array}\right.$.分析 根据加减消元法先将三元一次方程组转化为二元一次方程组,再转化为一元一次方程即可求得方程的解.
解答 解:$\left\{\begin{array}{l}{x-2y+4z=12}&{①}\\{3x+2y+z=1}&{②}\\{4x-z=7}&{③}\end{array}\right.$
由①+②,得
4x+5z=13④
由④-③,得
6z=6.
解得,z=1,
把z=1代入③,得 x=2,
把x=2,z=1代入①,解得,y=-3,
故原方程组的解是$\left\{\begin{array}{l}x=2\\ y=-3\\ z=1\end{array}\right.$.
点评 本题考查解三元一次方程组,解题的关键是明确解三元一次方程组的方法.

练习册系列答案
相关题目
20.若a>b,则下列不等式一定成立的是( )
| A. | a+b>b | B. | $\frac{b}{a}$>1 | C. | ac2>bc2 | D. | b-a<0 |
17.小强到体育用品商店购买羽毛球球拍和乒乓球球拍,已知购买1副羽毛球球拍和1副乒乓球球拍共需50元,小强一共用320元购买了6副同样的羽毛球拍和10副同样的乒乓球拍.若设每副羽毛球拍为x元,每副乒乓球拍为y元,根据题意,下面所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=50}\\{10(x+y)=320}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=50}\\{6x+10y=320}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=50}\\{6x+y=320}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=50}\\{10x+6y=320}\end{array}\right.$ |
4.甲乙两人在跳远练习中,6次成绩分别为(单位:米):
甲:3.8 3.8 3.9 3.9 4 4;
乙:3.8 3.9 3.9 3.9 3.9 4.
则这次跳远练习中,甲乙两人成绩方差的大小关系是( )
甲:3.8 3.8 3.9 3.9 4 4;
乙:3.8 3.9 3.9 3.9 3.9 4.
则这次跳远练习中,甲乙两人成绩方差的大小关系是( )
| A. | s2甲>s2乙 | B. | s2甲<s2乙 | C. | s2甲=s2乙 | D. | 无法确定 |
1.商店出售下列形状的地砖:
①长方形;②正方形;③正五边形;④正六边形.
若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有( )
①长方形;②正方形;③正五边形;④正六边形.
若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
18.下列各式是最简二次根式的为( )
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{a}{5}}$ | C. | $\sqrt{8a}$ | D. | $\sqrt{10a}$ |
19.为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如表(单位:秒):
(1)计算甲、乙两种电子钟走时误差的平均数;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 九 | 十 |
| 甲种电子钟 | 1 | -3 | -4 | 4 | 2 | -2 | 2 | -1 | -1 | 2 |
| 乙种电子钟 | 4 | -3 | -1 | 2 | -2 | 1 | -2 | 2 | -2 | 1 |
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
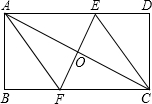 如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.
如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.