题目内容
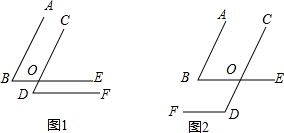
19.如图,∠B、∠D的两边分别平行.(1)如图1,∠B与∠D的数量关系是相等,说明理由,写出推理过程;
(2)如图2,直接写出∠B与∠D的数量关系是互补;
(3)由(1)、(2)归纳得出结论为:如果两个角的两条边分别平行,那么这两个角的关系是相等或互补..
分析 本题主要利用两直线平行,同位角相等;两直线平行,同旁内角互补及两直线平行,内错角相等进行解答.
解答  解:(1)相等;
解:(1)相等;
理由:图(1)中,∵AB∥CD,
∴∠B=∠1,
∵BE∥DF,
∴∠1=∠D,
∴∠B=∠D.
(2)互补;
理由:图(2)中,∵AB∥CD,
∴∠B=∠2,
∵BE∥DF,
∴∠2+∠D=180°,
∴∠B+∠D=180°.
(3)由(1)、(2)归纳得出结论为:
如果两个角的两条边分别平行,那么这两个角的关系是相等或互补.
故答案为:相等,互补,如果两个角的两条边分别平行,那么这两个角的关系是相等或互补.
点评 本题主要考查对平行线的性质的理解和运用,根据平行线的性质进行证明是解此题的关键.解题时注意:如果两个角的两条边分别平行,那么这两个角的关系是相等或互补.

练习册系列答案
相关题目
10.下列式子运算结果为x+1的是( )
| A. | $\frac{{x}^{2}-1}{x}$$•\frac{x}{x+1}$ | B. | 1-$\frac{1}{x}$ | C. | $\frac{{x}^{2}+2x+1}{x+1}$ | D. | $\frac{x+1}{x}$÷$\frac{1}{x-1}$ |
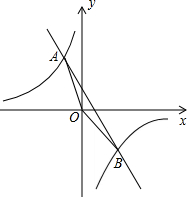 如图,反比例函数y=$\frac{k-1}{x}$(k<0)与一次函数y=kx+b相交于A、B两点,若点A的坐标为(-1,7).
如图,反比例函数y=$\frac{k-1}{x}$(k<0)与一次函数y=kx+b相交于A、B两点,若点A的坐标为(-1,7).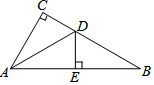 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,若AC=3cm,AB=5cm,则DE=$\frac{3}{2}$cm.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,若AC=3cm,AB=5cm,则DE=$\frac{3}{2}$cm.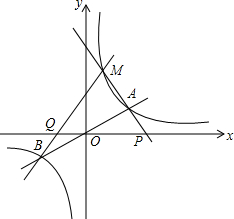 如图,已知双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x(k1,k2都为常数)相交于A,B两点,在第一象限内双曲线y=$\frac{{k}_{1}}{x}$上有一点M(M在A的左侧),设直线MA,MB分别与x轴交于P,Q两点,若MA=m•AP,MB=n•QB,则n-m的值是2.
如图,已知双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x(k1,k2都为常数)相交于A,B两点,在第一象限内双曲线y=$\frac{{k}_{1}}{x}$上有一点M(M在A的左侧),设直线MA,MB分别与x轴交于P,Q两点,若MA=m•AP,MB=n•QB,则n-m的值是2.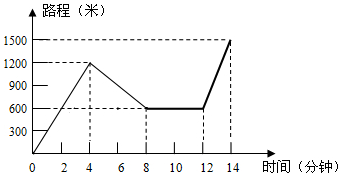 小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题: