题目内容
8.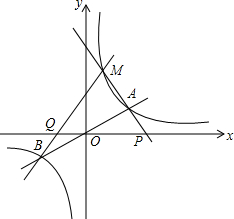 如图,已知双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x(k1,k2都为常数)相交于A,B两点,在第一象限内双曲线y=$\frac{{k}_{1}}{x}$上有一点M(M在A的左侧),设直线MA,MB分别与x轴交于P,Q两点,若MA=m•AP,MB=n•QB,则n-m的值是2.
如图,已知双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x(k1,k2都为常数)相交于A,B两点,在第一象限内双曲线y=$\frac{{k}_{1}}{x}$上有一点M(M在A的左侧),设直线MA,MB分别与x轴交于P,Q两点,若MA=m•AP,MB=n•QB,则n-m的值是2.
分析 作MH⊥y轴,AN⊥y轴,BI⊥y轴分别于点H、N、I,则MH∥AN∥BI,ON=OI,根据平行线分线段成比例定理即可求解.
解答  解:作MH⊥y轴,AN⊥y轴,BI⊥y轴分别于点H、N、I,则MH∥AN∥BI.
解:作MH⊥y轴,AN⊥y轴,BI⊥y轴分别于点H、N、I,则MH∥AN∥BI.
∵反比例函数是中心对称图形,
∴ON=OI.
∵MH∥AN∥BI,MA=m•AP,MB=n•QB
∴m=$\frac{MA}{AP}$=$\frac{HN}{ON}$,n=$\frac{MB}{BQ}$=$\frac{HI}{OI}$=$\frac{HN+ON+OI}{OI}$,
又∵ON=OI,
∴n=$\frac{HN+2ON}{ON}$=$\frac{HN}{ON}$+2=m+2,
∴n-m=2.
故答案是:2.
点评 本题考查了平行线分线段成比例定理和一次函数与反比例函数的应用,关键是根据平行线分线段成比例定理得出比例式,题目比较好,但有一定的难度.

练习册系列答案
相关题目
16.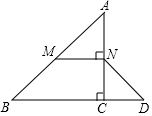 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DN、MN.若AB=6.
如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DN、MN.若AB=6.
(1)求证:MN=CD;
(2)求DN的长.
 如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DN、MN.若AB=6.
如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=$\frac{1}{3}$BD,连接DN、MN.若AB=6.(1)求证:MN=CD;
(2)求DN的长.
20.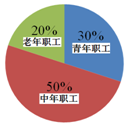 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
表2:小王抽样调查单位10名职工的健康指数
表3:小李抽样调查单位10名职工的健康指数
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
| 年龄 | 26 | 42 | 57 |
| 健康指数 | 97 | 79 | 72 |
| 年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
| 健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
| 年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
| 健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
 如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0),且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(-2,1)和点B.
如图,一次函数y=kx+b(k≠0)的图象过点P(-$\frac{3}{2}$,0),且与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A(-2,1)和点B.