题目内容
3. 已知M是菱形ABCD的对角线AC上一动点,连接BM并延长,交AD于点E,已知AB=5,AC=8,则当AM的长为4或$\frac{7}{4}$时,△BMC是直角三角形.
已知M是菱形ABCD的对角线AC上一动点,连接BM并延长,交AD于点E,已知AB=5,AC=8,则当AM的长为4或$\frac{7}{4}$时,△BMC是直角三角形.
分析 首先连接BD,交AC于点O,由菱形ABCD中,AB=5,AC=8,易求得BC=5,OA=OC=4,且BD⊥AC;然后分别从BM⊥AC与BM⊥BC去分析求解即可求得答案.
解答 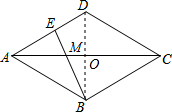 解:连接BD,交AC于点O,
解:连接BD,交AC于点O,
∵菱形ABCD中,AB=5,AC=8,
∴BC=AC=5,OA=OC=$\frac{1}{2}$AC=4,AC⊥BD;
当BM⊥AC时,点M与点O重合,此时AM=OA=4;
当BM⊥BC时,∠CBM=∠COB,∠BCM=∠OCB,
∴△CBM∽△COB,
∴$\frac{BC}{OC}=\frac{CM}{CB}$,
即$\frac{5}{4}=\frac{CM}{5}$,
∴CM=$\frac{25}{4}$,
∴AM=AC-CM=$\frac{7}{4}$;
综上:AM=4或$\frac{7}{4}$.
故答案为:4或$\frac{7}{4}$.
点评 此题考查了菱形的性质、相似三角形的判定与性质以及直角三角形的性质.注意准确作出辅助线,利用分类讨论思想求解是解此题的关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
14. 如图,直线y=-x+c与直线y=ax+b的交点坐标为(3,-1),关于x的不等式-x+c≥ax+b的解集为( )
如图,直线y=-x+c与直线y=ax+b的交点坐标为(3,-1),关于x的不等式-x+c≥ax+b的解集为( )
 如图,直线y=-x+c与直线y=ax+b的交点坐标为(3,-1),关于x的不等式-x+c≥ax+b的解集为( )
如图,直线y=-x+c与直线y=ax+b的交点坐标为(3,-1),关于x的不等式-x+c≥ax+b的解集为( )| A. | x≥-1 | B. | x≤-1 | C. | x≥3 | D. | x≤3 |
18.二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)中的x与y的部分对应值如下表所示,则下列结论中,正确的个数有( )
(1)a<0;
(2)当x<0时,y<3;
(3)当x>1时,y的值随x值的增大而减小;
(4)方程ax2+bx+c=5有两个不相等的实数根.
| x | -1 | 0 | 1 | 3 |
| y | -1 | 3 | 5 | 3 |
(2)当x<0时,y<3;
(3)当x>1时,y的值随x值的增大而减小;
(4)方程ax2+bx+c=5有两个不相等的实数根.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 如图,已知点C在线段AB上,点M、N分别是AC、BC的中点,且AB=8cm,则MN的长度为( )cm.
如图,已知点C在线段AB上,点M、N分别是AC、BC的中点,且AB=8cm,则MN的长度为( )cm.