题目内容
5．小明统计了他家今年11月份打电话的次数及通话时间，并列出了频数分布表：| 通话时间x/min | 0＜x≤5 | 5＜x≤10 | 10＜x≤15 | 15＜x≤20 |
| 频数（通话次数） | 19 | 16 | 5 | 10 |
| A． | 0.1 | B． | 0.4 | C． | 0.5 | D． | 0.8 |
分析 首先求得统计的通话总次数以及不超过15min的次数，利用概率公式即可直接求解．
解答 解：统计的通话总次数是19+16+5+10=50（次），
不超过15min的次数是19+16+5=40（次），
则通话时间不超过15min的频率为$\frac{40}{50}$=0.8．
故选D．
点评 本题考查了频数分布表，根据统计表确定统计的通话总次数以及不超过15min的次数是关键．
练习册系列答案
名校课堂系列答案
相关题目
13．下列关于$\sqrt{5}$的叙述，错误的是（ ）
| A． | $\sqrt{5}$是有理数 | B． | 面积为5的正方形边长是$\sqrt{5}$ | ||
| C． | $\sqrt{5}$介于2和3之间 | D． | 在数轴上可以找到表示$\sqrt{5}$的点 |
10．
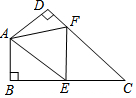在四边形ABCD中∠C=55°，∠B=∠D=90°，E，F分别是BC，DC上的点，当△EAF周长最小时，∠EAF的度数为（ ）
在四边形ABCD中∠C=55°，∠B=∠D=90°，E，F分别是BC，DC上的点，当△EAF周长最小时，∠EAF的度数为（ ）| A． | 55° | B． | 70° | C． | 125° | D． | 110° |
17．已知点D与点A（0，8），B（0，-2），C（x，y）是平行四边形的四个顶点，其中x，y满足x-y+6=0，则CD长的最小值为（ ）
| A． | $\frac{16}{5}$ | B． | $3\sqrt{2}$ | C． | $2\sqrt{2}$ | D． | 10 |
为争取一张“欧洲杯球友会”的入场券，现在有两种方案供你选择：