题目内容
9. 在等腰Rt△ABC中,AB=AC,∠DAE=45°,若BC=10,求BE•CD.
在等腰Rt△ABC中,AB=AC,∠DAE=45°,若BC=10,求BE•CD.
分析 易知∠B=∠C,只需再证明一对角相等即可.根据外角易证∠BAE=∠ADC.根据勾股定理,BC2=2AB2,所以需证AB2=BE•CD.进而解答即可.
解答 解:在Rt△ABC中,
∵AB=AC,
∴∠B=∠C=45°.
∵∠BAE=∠BAD+∠DAE,∠DAE=45°,
∴∠BAE=∠BAD+45°.
而∠ADC=∠BAD+∠B=∠BAD+45°,
∴∠BAE=∠CDA.
∴△ABE∽△DCA.
(2)由△ABE∽△DCA,得$\frac{BE}{AB}=\frac{AC}{CD}$.
∴BE•CD=AB•AC.
而AB=AC,BC2=AB2+AC2,
∴BC2=2AB2.
∴BC2=2BE•CD,
∴BE•CD=50
点评 此题考查了相似三角形的判定和性质,特别是与勾股定理联系起来综合性很强,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
 如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )| A. | 20° | B. | 60° | C. | 70° | D. | 80° |
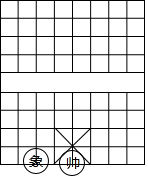 如图,中国象棋中对“象”的走法有一定的限制,只能走“田”字.若此时“象”的坐标为(-2,-4)“帅”的坐标为(0,-4),试写出此“象”下一步可能走到的各位置的坐标.
如图,中国象棋中对“象”的走法有一定的限制,只能走“田”字.若此时“象”的坐标为(-2,-4)“帅”的坐标为(0,-4),试写出此“象”下一步可能走到的各位置的坐标.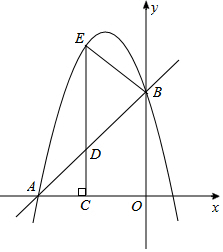 如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=-x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.
如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=-x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.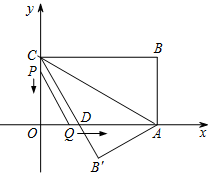 如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(6,0),将△ABC沿AC翻折,使点B落到点B′处,B′C交x轴于点D,且CD=2DB′.动点P从点C出发,沿CO以每秒1个单位的速度向点O运动;动点Q从点O出发,沿OA、AB以每秒3个单位的速度向点B运动,连接PQ.若P、Q两点同时出发,当其中一点到达终时整个运动随之结束,设运动时间为t秒.
如图,在平面直角坐标系中,矩形OABC的顶点A的坐标为(6,0),将△ABC沿AC翻折,使点B落到点B′处,B′C交x轴于点D,且CD=2DB′.动点P从点C出发,沿CO以每秒1个单位的速度向点O运动;动点Q从点O出发,沿OA、AB以每秒3个单位的速度向点B运动,连接PQ.若P、Q两点同时出发,当其中一点到达终时整个运动随之结束,设运动时间为t秒.