题目内容
9.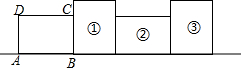 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )| A. | 2017π | B. | 2034π | C. | 3024π | D. | 3026π |
分析 首先求得每一次转动的路线的长,发现每4次循环,找到规律然后计算即可.
解答 解:∵AB=4,BC=3,
∴AC=BD=5,
转动一次A的路线长是:$\frac{90π×4}{180}$=2π,
转动第二次的路线长是:$\frac{90π×5}{180}$=$\frac{5}{2}$π,
转动第三次的路线长是:$\frac{90π×3}{180}$=$\frac{3}{2}$π,
转动第四次的路线长是:0,
以此类推,每四次循环,
故顶点A转动四次经过的路线长为:$\frac{5}{2}$π+$\frac{3}{2}$π+2π=6π,
∵2017÷4=504…1,
∴顶点A在整个旋转过程中所经过的路径总长为:6π×504+2π=3026π,
故选D.
点评 本题主要考查了探索规律问题和弧长公式的运用,掌握旋转变换的性质、灵活运用弧长的计算公式、发现规律是解决问题的关键.

练习册系列答案
相关题目
19.某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
| 售价x(元/千克) | 50 | 60 | 70 |
| 销售量y(千克) | 100 | 80 | 60 |
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入-成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
4. 如图,几何体是由3个完全一样的正方体组成,它的左视图是( )
如图,几何体是由3个完全一样的正方体组成,它的左视图是( )
 如图,几何体是由3个完全一样的正方体组成,它的左视图是( )
如图,几何体是由3个完全一样的正方体组成,它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
4.某蔬菜基地打算将115吨的蔬菜运往县城销售,现找到一物流公司有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示(假设每辆车均满载,并且每种车型数量足够):
(1)若全部蔬菜都用甲、乙两种车型来运送,需运费7800元,问分别需甲、乙两种车型各几辆?
(2)蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送,将全部蔬菜运往县城销售,如何安排装运,可使运费最省?最省运费是多少?
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
(2)蔬菜基地计划用甲、乙、丙三种车型共15辆同时参与运送,将全部蔬菜运往县城销售,如何安排装运,可使运费最省?最省运费是多少?
 如图,直线l1∥l2,∠1=20°,则∠2+∠3=200°.
如图,直线l1∥l2,∠1=20°,则∠2+∠3=200°. 如图,已知直线a∥b,∠1=70°,则∠2=110°.
如图,已知直线a∥b,∠1=70°,则∠2=110°.