题目内容
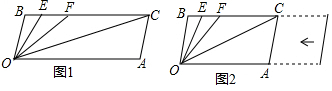
1.将直线y=3x+1向下平移1个单位长度,得到直线y=3x+m,若反比例函数y=$\frac{k}{x}$的图象与直线y=3x+m相交于点A,且点A的纵坐标是3.(1)求m和k的值;
(2)结合图象求不等式3x+m>$\frac{k}{x}$的解集.
分析 (1)根据平移的原则得出m的值,并计算点A的坐标,因为A在反比例函数的图象上,代入可以求k的值;
(2)画出两函数图象,根据交点坐标写出解集.
解答 解:(1)由平移得:y=3x+1-1=3x,
∴m=0,
当y=3时,3x=3,
x=1,
∴A(1,3),
∴k=1×3=3;
(2)画出直线y=3x和反比例函数y=$\frac{3}{x}$的图象:如图所示,
由图象得:不等式3x+m>$\frac{k}{x}$的解集为:-1<x<0或x>1.
点评 本题考查的是一次函数与反比例函数的交点问题和一次函数的图象的平移问题,涉及到用待定系数法求反比例函数的解析式,并熟知函数图象平移时“上加下减,左加右减”的法则.

练习册系列答案
相关题目
12.人教版初中数学教科书共六册,总字数是978000,用科学记数法可将978000表示为( )
| A. | 978×103 | B. | 97.8×104 | C. | 9.78×105 | D. | 0.978×106 |
9.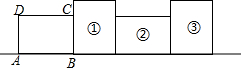 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )| A. | 2017π | B. | 2034π | C. | 3024π | D. | 3026π |
16.关于x的一元二次方程x2+8x+q=0有两个不相等的实数根,则q的取值范围是( )
| A. | q<16 | B. | q>16 | C. | q≤4 | D. | q≥4 |
6.若一组数据2,3,x,5,7的众数为7,则这组数据的中位数为( )
| A. | 2 | B. | 3 | C. | 5 | D. | 7 |
13.关于x的一元二次方程ax2+bx+c=0(a≠0)的两根为x1=1,x2=-1,那么下列结论一定成立的是( )
| A. | b2-4ac>0 | B. | b2-4ac=0 | C. | b2-4ac<0 | D. | b2-4ac≤0 |
 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为48+12$\sqrt{3}$.
已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为48+12$\sqrt{3}$.