题目内容
8．方程5x2-x-3=x2-3+x的二次项是4x2，二次项系数是4，一次项系数是-2，常数项是0．分析 根据移项、合并同类项，可得一元二次方程的一般形式，根据ax2+bx+c=0（a，b，c是常数且a≠0）特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．在一般形式中ax2叫二次项，bx叫一次项，c是常数项．其中a，b，c分别叫二次项系数，一次项系数，常数项，可得答案．
解答 解：移项、合并同类项，得
4x2-2x=0，
二次项是 4x2，二次项系数是 4，一次项系数是-2，常数项是 0，
故答案为：4x2，4，-2，0．
点评 本题考查了一元二次方程的一般形式，一元二次方程的一般形式是：ax2+bx+c=0（a，b，c是常数且a≠0）特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．在一般形式中ax2叫二次项，bx叫一次项，c是常数项．其中a，b，c分别叫二次项系数，一次项系数，常数项．
练习册系列答案
孟建平名校考卷系列答案
相关题目
12．已知a+b=$\sqrt{5}$，则$\frac{{a}^{2}-{a}^{2}{b}^{2}+{b}^{2}+2ab}{a+ab+b}$+ab等于（ ）
| A． | $\sqrt{5}$ | B． | $\frac{\sqrt{5}}{2}$ | C． | 2 | D． | 2$\sqrt{5}$ |
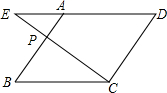如图，点P是平行四边形ABCD边AB上一点，且AB=3AP，连接CP，并延长CP、DA交于点E，则△AEP与△DEC的周长之比为1：3．
如图所示，在数轴上点A所表示的数为a，则a的值为-1-$\sqrt{5}$．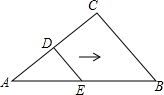
如图，D、E分别是AC和AB上的点，AD=DC=4，DE=3，DE∥BC，∠C=90°，将△ADE沿着AB边向右平移，当点D落在BC上时，平移的距离为5．
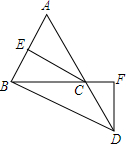如图，在△ABC中，延长AC至点D，使CD=BC，连接BD，作CE⊥AB于点E，DF⊥BC交BC的延长线于点F，且AB=AC．如果∠ABD=105°，∠A=40度．