题目内容
17.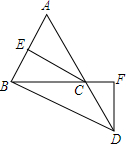 如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且AB=AC.如果∠ABD=105°,∠A=40度.
如图,在△ABC中,延长AC至点D,使CD=BC,连接BD,作CE⊥AB于点E,DF⊥BC交BC的延长线于点F,且AB=AC.如果∠ABD=105°,∠A=40度.
分析 由CD=BC,可得∠CBD=∠CDB,然后由三角形的外角的性质可得:∠ACB=∠CBD+∠CDB=2∠CBD,由∠ABC=∠ACB,进而可得:∠ABC=2∠CBD,然后由∠ABD=∠ABC+∠CBD=3∠CBD=105°,进而可求:∠CBD的度数及∠ABC的度数,然后由三角形的内角和定理即可求∠A的度数.
解答 解:∵CD=BC,
∴∠CBD=∠CDB,
∵∠ACB=∠CBD+∠CDB,
∴∠ACB=2∠CBD,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC=2∠CBD,
∵∠ABD=∠ABC+∠CBD=3∠CBD=105°,
∴∠CBD=35°,
∴∠ABC=2∠CBD=70°,
∴∠A=180°-2∠ABC=40°,
故答案为:40.
点评 本题考查了等腰三角形的性质,三角形外角的性质,三角形的内角和,熟练掌握等腰三角形的性质是解题的关键.

练习册系列答案
相关题目
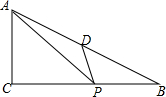 如图,Rt△ABC中,∠C=90°,∠B=30°,BC=8,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是8.
如图,Rt△ABC中,∠C=90°,∠B=30°,BC=8,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是8.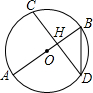 如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则BH的长为( )
如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则BH的长为( )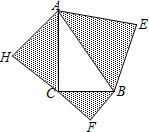 已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=8,则图中阴影部分的面积为32.
已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=8,则图中阴影部分的面积为32.


 如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC.
如图,AB是⊙O的直径,CB是弦,OD⊥CB于E,交$\widehat{CB}$于D,连接AC.