题目内容
19.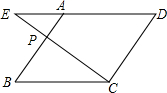 如图,点P是平行四边形ABCD边AB上一点,且AB=3AP,连接CP,并延长CP、DA交于点E,则△AEP与△DEC的周长之比为1:3.
如图,点P是平行四边形ABCD边AB上一点,且AB=3AP,连接CP,并延长CP、DA交于点E,则△AEP与△DEC的周长之比为1:3.
分析 先根据平行四边形的性质得AB∥CD,AB=CD,再由AB=3AP得到CD=3AP,接着根据相似三角形的判定易得△AEP∽△DEC,然后根据相似三角形的性质求△AEP与△DEC的周长之比.
解答 解:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD,
∵AB=3AP,
∴CD=3AP,
∵AP∥DC,
∴△AEP∽△DEC,
∴△AEP与△DEC的周长之比=AP:CD=1:3.
故答案为1:3.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了平行四边形的性质.

练习册系列答案
相关题目
14.下列说法中不正确的是( )
| A. | 要反映我市一周内每天的最低气温的变化情况宜采用折线统计图 | |
| B. | 打开收音机正在播放TFBOYS的歌曲是必然事件 | |
| C. | 方差反映了一组数据的稳定程度 | |
| D. | 为了解一种灯泡的使用寿命.应采用抽样调查的办法 |
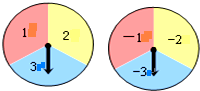 如图,有转盘A、B分别被分成三个面积相等的扇形,上面分别写有3个数字,用力转动两个转盘,转盘上的指针分别指向一个数字,则两个转盘指针指向的两个数之和恰好为0的概率是$\frac{1}{3}$.
如图,有转盘A、B分别被分成三个面积相等的扇形,上面分别写有3个数字,用力转动两个转盘,转盘上的指针分别指向一个数字,则两个转盘指针指向的两个数之和恰好为0的概率是$\frac{1}{3}$.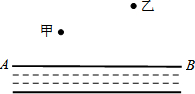 小河AB的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.若要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?(要求:不写作法,但要保留作图痕迹,并写出作图结果)
小河AB的同旁有甲、乙两个村庄,现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.若要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?(要求:不写作法,但要保留作图痕迹,并写出作图结果)