题目内容
13.已知抛物线y=x2+bx+c,经过点A(0,5)和点B(3,2).(1)求抛物线的解析式;
(2)指出它的开口方向,对称轴和顶点坐标.
分析 (1)把点A、B的坐标代入函数解析式,根据待定系数法列式求解即可.
(2)根据a的符号确定开口方向,把一般式化成顶点式即可求得对称轴和顶点坐标.
解答 解:(1)∵抛物线y=x2+bx+c经过点A(0,5)和B(3,2)点,
∴$\left\{\begin{array}{l}{c=5}\\{9+3b+c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-4}\\{c=5}\end{array}\right.$,
∴抛物线的解析式是:y=x2-4x+5.
(2)∵y=x2-4x+5=(x-2)2+1,a=1
∴抛物线的开口向上,对称轴为x=2,顶点坐标为(2,1).
点评 此题考查了待定系数法求二次函数解析式以及二次函数的性质,利用已知点的坐标代入解析式求出是解题关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
3.(1)先求出下列各组数据的平均数和方差;
①1,2,3,4,5,6,7,8,9;
②11,12,13,14,15,16,17,18,19,;
③10,20,30,40,50,60,70,80,90.
(2)根据上面的计算结果,你能发现什么规律,按你的发现填写下表:
①1,2,3,4,5,6,7,8,9;
②11,12,13,14,15,16,17,18,19,;
③10,20,30,40,50,60,70,80,90.
(2)根据上面的计算结果,你能发现什么规律,按你的发现填写下表:
| 数 据 | 平均数 | 方差 |
| x1,x2,…,xn | $\overline{X}$ | S2 |
| x1+a,x2+a,…,xn+a | $\overline{x}$+a | S2 |
| mx1,mx2,…,mxn | m$\overline{x}$ | m2S2 |
1.随意掷两个均匀的骰子,朝上面的点数之和是10的概率是( )
| A. | $\frac{1}{12}$ | B. | 1 | C. | $\frac{1}{18}$ | D. | 0 |
3.下列计算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | -42=16 | C. | $\root{3}{-8}$=-2 | D. | 87=56 |
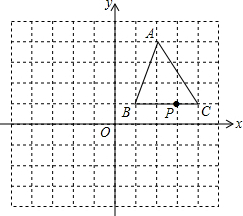 如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.
如图,三角形ABC的顶点坐标分别为A(2,4)、B(1,1)、C(4,1).BC上的一点P的坐标为P(3,1),将三角形ABC向左平移4个单位,再向上平移1个单位,得到三角形A1B1C1,其中点A、B、C、P分别对应点A1、B1、C1、P1.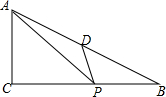 如图,Rt△ABC中,∠C=90°,∠B=30°,BC=8,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是8.
如图,Rt△ABC中,∠C=90°,∠B=30°,BC=8,D为AB的中点,P为BC上一个动点,连接AP,DP,则AP+DP的最小值是8.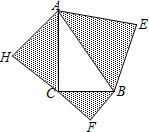 已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=8,则图中阴影部分的面积为32.
已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=8,则图中阴影部分的面积为32.