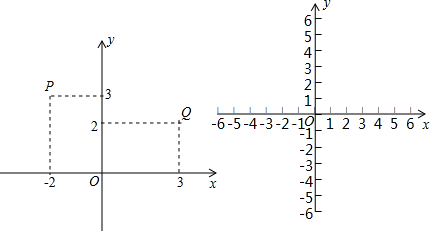题目内容
3.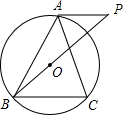 如图,⊙O是△ABC的外接圆,弧AB=弧AC,AP是⊙O的切线,交BO的延长线于点P.
如图,⊙O是△ABC的外接圆,弧AB=弧AC,AP是⊙O的切线,交BO的延长线于点P.(1)求证:AP∥BC;
(2)若tan∠P=$\frac{3}{4}$,求tan∠PAC的值.
分析 (1)作AH⊥BC于H,如图,利用弧、弦、圆周角之间的关系由弧AB=弧AC得到AB=AC,则根据等腰三角形的性质得BH=CH,再根据垂径定理的推论可判断点O在AH上,然后根据切线的性质得OA⊥AP,于是可判断AP∥BC;
(2)根据平行线的性质,由AP∥BC得到∠P=∠PBC,再根据正切的定义得到tan∠OBH=$\frac{OH}{BH}$=$\frac{3}{4}$,设OH=3x,则BH=4x,OB=5x,然后在Rt△ABH中利用正切的定义可计算出tan∠ABH=2,然后证明∠ABH=∠C=∠PAC即可.
解答 (1)证明:作AH⊥BC于H,如图,
∵弧AB=弧AC,
∴AB=AC,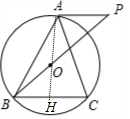
∴BH=CH,
即AH垂直平分BC,
∴点O在AH上,
∵AP为切线,
∴OA⊥AP,
∴AP∥BC;
(2)解:∵AP∥BC,
∴∠P=∠PBC,
在Rt△OBH中,tan∠OBH=$\frac{OH}{BH}$=$\frac{3}{4}$,
设OH=3x,则BH=4x,
∴OB=5x,
∴AH=OA+OH=8x,
在Rt△ABH中,tan∠ABH=$\frac{AH}{BH}$=$\frac{8x}{4x}$=2,
∵∠ABH=∠C=∠PAC,
∴tan∠PAC=2.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了等腰三角形的性质和垂径定理.

练习册系列答案
相关题目
15.已知函数y=ax2-2ax-1(a是常数,a≠0),下列结论正确的是( )
| A. | 当a=1时,函数图象经过点(-1,1) | |
| B. | 当a=-2时,函数图象与x轴没有交点 | |
| C. | 若a<0,函数图象的顶点始终在x轴的下方 | |
| D. | 若a>0,则当x≥1时,y随x的增大而增大 |
14.与$\sqrt{5}$可以合并的二次根式是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{15}$ | C. | $\sqrt{20}$ | D. | $\sqrt{25}$ |
11.下列说法错误的是( )
| A. | 平移和旋转都不改变图形的形状和大小 | |
| B. | 成中心对称的两个图形中,对应点连线的中点是对称中心 | |
| C. | 在平移和旋转图形的过程中,对应角相等,对应线段相等且平行 | |
| D. | 一个图形和它经过旋转后所得的图形中,对应点到旋转中心的距离相等 |
12.在实数-3,2,0,-1中,最小的数是( )
| A. | -3 | B. | 2 | C. | 0 | D. | -1 |
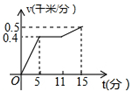
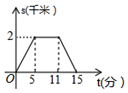

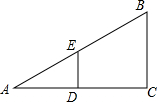 如图,在Rt△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC,交AB于点E,交AC于点D,则DE的长为( )
如图,在Rt△ABC中,∠ACB=90°,AC=8,AB=10,DE垂直平分AC,交AB于点E,交AC于点D,则DE的长为( ) 如图,抛物线y=-x2-2x+3的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
如图,抛物线y=-x2-2x+3的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.