题目内容
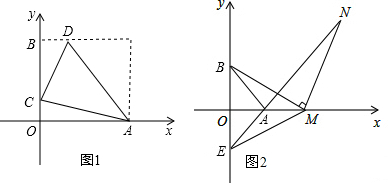
2. 如图所示,在Rt△ABC中,∠C=90°,D是BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,求AC的长.
如图所示,在Rt△ABC中,∠C=90°,D是BC上一点,∠DAC=30°,BD=2,AB=2$\sqrt{3}$,求AC的长.
分析 首先用未知数表示出DC,AC的长,进而利用勾股定理得出AC的长.
解答 解:设DC=x,
∵∠DAC=30°,
∴AC=$\sqrt{3}$x,
∴在在Rt△ABC中,AC2+BC2=AB2,
即(2$\sqrt{3}$)2=(2+x)2+($\sqrt{3}$x)2,
解得:x=2或-1(负数舍去),
故AC=$\sqrt{3}$x=2$\sqrt{3}$,
则AC的长为2$\sqrt{3}$.
点评 此题主要考查了勾股定理以及含30度角的直角三角形,正确表示出AC的长是解题关键.

练习册系列答案
相关题目
7.图中的各曲线中,不表示y是x的函数是( )
| A. |  | B. |  | C. |  | D. |  |
12.计算题.
| (1)(-2)+(-7); | (2)-32-5; | (3)(-30.5)×0.2; |
| (4)12-(-18)+(-7)-15; | (5)(-$\frac{3}{4}$)×(-1$\frac{1}{2}$)×0÷(-2$\frac{1}{4}$); | (6)-9×(-11)÷3÷(-3); |
| (7)-18÷2$\frac{1}{4}$-$\frac{4}{9}$÷(-$\frac{2}{3}$); | (8)($\frac{9}{10}$-$\frac{2}{15}$+$\frac{1}{6}$)×30; | (9)1-3.9÷[1-$\frac{3}{4}$-(-0.5)]. |
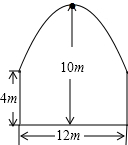 如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m,隧道顶部最高点距地面10m.在抛物线型拱壁上需要安装两排灯.使它们离地面的高度相等,如果灯离地面的高度为8m,那么两排灯之间的水平距离是多少米?
如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m,隧道顶部最高点距地面10m.在抛物线型拱壁上需要安装两排灯.使它们离地面的高度相等,如果灯离地面的高度为8m,那么两排灯之间的水平距离是多少米?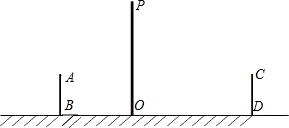 如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.