题目内容
15.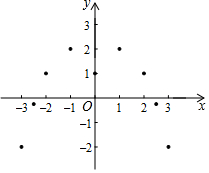 某“数学兴趣小组”根据学习函数的经验,对函数y=-x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整:
某“数学兴趣小组”根据学习函数的经验,对函数y=-x2+2|x|+1的图象和性质进行了探究,探究过程如下,请补充完整:(1)自变量x的取值范围是全体实数,x与y的几组对应数值如表:
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | -2 | -$\frac{1}{4}$ | m | 2 | 1 | 2 | 1 | -$\frac{1}{4}$ | -2 | … |
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)根据函数图象,写出:
①该函数的一条性质函数图象关于y轴对称;
②直线y=kx+b经过点(-1,2),若关于x的方程-x2+2|x|+1=kx+b有4个互不相等的实数根,则b的取值范围是1<b<2.
分析 (1)把x=-2代入函数解释式即可得m的值;
(2)描点、连线即可得到函数的图象;
(3)①根据函数图象得到函数y=x2-2|x|+1的图象关于y轴对称;当x>1时,y随x的增大而减少;
②根据函数的图象即可得到b的取值范围是1<b<2.
解答 解:(1)当x=-2时,m=-(-2)2+2×|-2|+1=-4+4+1=1.
(2)如图所示:
(3)①答案不唯一.如:函数图象关于y轴对称.
②由函数图象知:∵关于x的方程-x2+2|x|+1=kx+b有4个互不相等的实数根,
∴b的取值范围是1<b<2.
故答案为:1;函数图象关于y轴对称;1<b<2.
点评 本题考查了抛物线与x轴的交点,二次函数的图象和性质,正确的识别图象是解题的关键.

练习册系列答案
相关题目
3.下列各式中,从左到右的变形是因式分解的是( )
| A. | 3x+3y+1=3(x+y)+1 | B. | a2-2a+1=(a-1)2 | C. | (m+n)(m-n)=m2-n2 | D. | x(x-y)=x2-xy |
10. 《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是( )
 《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有这样一个问题:“今有勾八步,股十五步,问勾中容圆,径几何?”其意思是:“如图,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”此问题中,该内切圆的直径是( )| A. | 5步 | B. | 6步 | C. | 8步 | D. | 10步 |
7.某公司产销一种产品,为保证质量,每个周期产销商品件数控制在100以内,产销成本C是商品件数x的二次函数,调查数据如表:
商品的销售价格(单位:元)为P=35-$\frac{1}{10}$x(每个周期的产销利润=P•x-C)
(1)直接写出产销成本C与商品件数x的函数关系式(不要求写出自变量的取值范围)
(2)该公司每个周期产销多少件商品时,利润达到220元?
(3)求该公司每个周期的产销利润的最大值.
| 产销商品件数(x/件) | 10 | 20 | 30 |
| 产销成本(C/元) | 120 | 180 | 260 |
(1)直接写出产销成本C与商品件数x的函数关系式(不要求写出自变量的取值范围)
(2)该公司每个周期产销多少件商品时,利润达到220元?
(3)求该公司每个周期的产销利润的最大值.


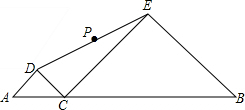 如图,线段AB长为6,点C是线段AB上一动点(不与A,B重合)分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1处沿AB向右运动至距离B点1处时,点P运动的路径长是2.
如图,线段AB长为6,点C是线段AB上一动点(不与A,B重合)分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1处沿AB向右运动至距离B点1处时,点P运动的路径长是2.