题目内容
16. 如图,直线AB与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若$\frac{1}{3}$<u<2,求v的取值范围.
如图,直线AB与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A(u,p)和点B(v,q),与x轴交于点C,已知∠ACO=45°,若$\frac{1}{3}$<u<2,求v的取值范围.
分析 由∠ACO=45°,可设直线AB的解析式为y=-x+b.由点A、B在反比例函数图象上,可得出“p=$\frac{4}{u}$,q=$\frac{4}{v}$”,将其代入点A、B的坐标中,再利用点A、B在直线AB上,可得出“$\frac{4}{u}$=-u+b①,$\frac{4}{v}$=-v+b②”,二者做差即可得出u、v的关系,结合点u的取值范围即可得出结论.
解答 解:∵∠ACO=45°,
∴设直线AB的解析式为y=-x+b.
∵点A(u,p)和点B(v,q)为反比例函数y=$\frac{4}{x}$(x>0)的图象上的点,
∴p=$\frac{4}{u}$,q=$\frac{4}{v}$,
∴点A(u,$\frac{4}{u}$),点B(v,$\frac{4}{v}$).
又∵点A、B为直线AB上的点,
∴$\frac{4}{u}$=-u+b①,$\frac{4}{v}$=-v+b②,
①-②得:$\frac{4(v-u)}{uv}$=v-u,
即v=$\frac{4}{u}$.
又∵$\frac{1}{3}$<u<2,
∴2<v<12.
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是找出v=$\frac{4}{u}$.本题属于基础题,难度不大,解决该题型题目时,对直线AB解析式设而不求,利用点在反比例函数图象上,分别找出其坐标特点,再将其代入一次函数解析中,通过计算即可得出结论.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
1.下列事件为必然事件的是( )
| A. | 打开电视机,它正在播广告 | |
| B. | 某彩票的中奖机会是1%,买1张一定不会中奖 | |
| C. | 抛掷一枚硬币,一定正面朝上 | |
| D. | 投掷一枚普通的正方体骰子,掷得的点数小于7 |
6.某校九年级两个班,各选派10名学生参加学校举行的“数学奥林匹克”大赛预赛.各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
(1)直接写出表中a、b的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
| 九(1)班 | 100 | 94 | b | 93 | 12 |
| 九(2)班 | 99 | a | 95.5 | 93 | 8.4 |
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,求另外两个决赛名额落在不同班级的概率.
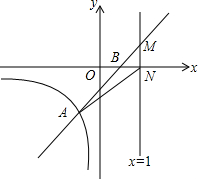 直线y=kx+b与反比例函数y=$\frac{2}{x}$(x<0)的图象交于点A(-1,m),与x轴交于点B(1,0)
直线y=kx+b与反比例函数y=$\frac{2}{x}$(x<0)的图象交于点A(-1,m),与x轴交于点B(1,0) 如图,已知等边△ABO在平面直角坐标系中,点A(4$\sqrt{3}$,0),函数y=$\frac{k}{x}$(x>0,k为常数)的图象经过AB的中点D,交OB于E.
如图,已知等边△ABO在平面直角坐标系中,点A(4$\sqrt{3}$,0),函数y=$\frac{k}{x}$(x>0,k为常数)的图象经过AB的中点D,交OB于E. 如图,以?ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AE,则四边形AOCD的面积是9.
如图,以?ABCO的顶点O为原点,边OC所在直线为x轴,建立平面直角坐标系,顶点A、C的坐标分别是(2,4)、(3,0),过点A的反比例函数y=$\frac{k}{x}$的图象交BC于D,连接AE,则四边形AOCD的面积是9. 如图,在以BC为直径的半圆O中,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.
如图,在以BC为直径的半圆O中,∠BCD的平分线交⊙O于F,E为CF延长线上一点,且∠EBF=∠GBF.