题目内容
12．
如图，点C是线段AB上一点，AC＜AB，M，N分别是AB和CB的中点，AC=8，NB=5，求线段MN的长．
分析 根据线段中点的性质，可得BC的长，根据线段的和差，可得AB的长，再根据线段中点的性质，可得BM的长，根据线段的和差，可得答案．
解答 解：由N是CB的中点，NB=5，得
BC=2NB=10．
由线段的和差，得
AB=AC+BC=8+10=18．
由M是AB的中点，得
MB=$\frac{1}{2}$AB=$\frac{1}{2}$×18=9．
由线段的和差，得
MN=MB-NB=9-5=4．
点评 本题考查了两点间的距离，利用线段中点的性质得出MB的长是解题关键．
练习册系列答案
全能练考卷系列答案
相关题目
18．下列选项中，是方程x-2y=2的解是（ ）
| A． | $\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ |
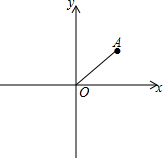如图，在直角坐标系中，O是坐标原点，且点A坐标为（4，4），P是y轴上的一点，若以O，A，P三点组成的三角形为等腰三角形，求P点的坐标．
如图，已知在Rt△ABC中，∠ACB=90°，点D为AB中点，CD=5，sinA=$\frac{3}{5}$，则BC=6．
4．
如图，在△ABC中，点D在BC上，且BD=2CD，AB⊥AD，若tanB=$\frac{4}{3}$，则tan∠CAD=（ ）
如图，在△ABC中，点D在BC上，且BD=2CD，AB⊥AD，若tanB=$\frac{4}{3}$，则tan∠CAD=（ ）| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{1}{4}$ | C． | $\sqrt{3}$ | D． | $\frac{1}{3}$ |
如图，⊙O的直径CD=10，AB是⊙O的弦，AB⊥CD，垂足为M，OM：MC=3：2，则AB的长等于8．