题目内容
7.某工厂大门是抛物线形水泥建筑物,大门宽为4m,顶部距地面的高度为4.4m,现有一辆满载货物的汽车欲通过大门,其装货宽度为2.4m,该车要想通过此门,装货后的最大高度应为( )| A. | 2.80m | B. | 2.816m | C. | 2.82m | D. | 2.826m |
分析 根据题意可以画出相应的抛物线,然后根据待定系数法求出抛物线的解析式,再根据题目中的数据即可求得该车要想通过此门,装货后的最大高度.
解答  解:如有右图所示,
解:如有右图所示,
设AB=4m,CH=4.4,EF=2.4,
设此抛物线的解析式为y=kx2,
则点A(-2,-4.4)在此抛物线上,
∴-4.4=k×(-2)2,
得k=-1.1,
∴y=-1.1x2,
∵点E的横坐标为-1.2,
则y=-1.1×(-1.2)2,得y=-1.584,
∴该车要想通过此门,装货后的最大高度应为:(-1.584)-(-4.4)=2.816m,
故选B.
点评 本题考查二次函数的应用,解答本题的关键是画出相应的抛物线,利用抛物线的性质和数形结合的思想解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.小明饶着一个五边形的花圃走了一圈,他一共转了多少度( )
| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
17.已知|a|=2,|b|=3,且|a+b|=|a|+|b|,则a+b的值为( )
| A. | 5 | B. | ±5 | C. | 1 | D. | ±1 |
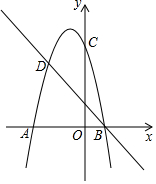 已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).
已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).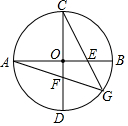 如图,已知圆O的直径AB与CD互相垂直,E为OB中点,CE的延长线交圆O于G,AG交CD于F,求$\frac{DF}{FC}$的值.
如图,已知圆O的直径AB与CD互相垂直,E为OB中点,CE的延长线交圆O于G,AG交CD于F,求$\frac{DF}{FC}$的值.