题目内容
1.已知二次函数y=x2-5x+m(m为实数)的图象与x轴上的一个交点为(2,0),则关于x的一元二次方程x2-5x+m=0的两实数根是( )| A. | x1=2,x2=-2 | B. | x1=2,x2=3 | C. | x1=2,x2=0 | D. | x1=2,x2=-3 |
分析 根据抛物线与x轴交点的性质和根与系数的关系进行解答.
解答 解:∵y=x2-5x+m(m为实数)的图象与x轴上的一个交点为(2,0),
∴关于x的一元二次方程x2-5x+m=0的一个根是x=2.
∴设关于x的一元二次方程x2-5x+m=0的另一根是t.
∴2+t=5,
解得 t=3.
即方程的另一根为3.
故选B.
点评 本题考查了抛物线与x轴的交点.注意二次函数解析式与一元二次方程间的转化关系.

练习册系列答案
相关题目
 二次函数y=2x2+mx+8的图象如图所示,则方程2x2+mx+8=0的根为( )
二次函数y=2x2+mx+8的图象如图所示,则方程2x2+mx+8=0的根为( )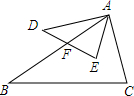 如图,已知△ABC与△ADE中,则∠C=∠E,∠DAB=∠CAE,∠D=∠B,$\frac{AF}{AC}$=$\frac{AD}{AB}$,$\frac{DE}{BC}$=$\frac{AE}{AC}$,$\frac{AD}{AE}$=$\frac{AB}{AC}$,则下列各式成立的个数是( )
如图,已知△ABC与△ADE中,则∠C=∠E,∠DAB=∠CAE,∠D=∠B,$\frac{AF}{AC}$=$\frac{AD}{AB}$,$\frac{DE}{BC}$=$\frac{AE}{AC}$,$\frac{AD}{AE}$=$\frac{AB}{AC}$,则下列各式成立的个数是( ) 将一副直角三角板如图放置,若AE∥BC,则∠CAD的度数是15°.
将一副直角三角板如图放置,若AE∥BC,则∠CAD的度数是15°.