题目内容
11.计算:(1)tan60°+|2-$\sqrt{3}$|-3-2;
(2)解分式方程:$\frac{2x+2}{3x-5}$-4=0.
分析 (1)本题涉及特殊角的三角函数值、绝对值、负整数指数幂、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)公分母为(3x-5),两边同乘以公分母,转化为整式方程求解,结果要检验.
解答 解:(1)原式=$\sqrt{3}$+2-$\sqrt{3}$-$\frac{1}{9}$
=$\frac{17}{9}$;
(2)去分母,得2x+2-4(3x-5)=0,
去括号,得2x+2-12x+20=0,
合并,得-10x+22=0,
解得x=2.2,
经检验x=2.2是原方程的解,
故原方程的解为x=2.2.
点评 本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、二次根式、绝对值等考点的运算.同时考查了解分式方程.

练习册系列答案
相关题目
2.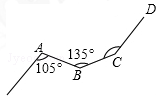 如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角A是105°,第二才拐的角B是135°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C的度数为( )
如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角A是105°,第二才拐的角B是135°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C的度数为( )
 如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角A是105°,第二才拐的角B是135°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C的度数为( )
如图,一条铁路修到一个村子边时,需拐弯绕道而过,如果第一次拐的角A是105°,第二才拐的角B是135°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,那么∠C的度数为( )| A. | 130° | B. | 135° | C. | 140° | D. | 150° |
20. 如图,镜子中号码的实际号码是( )
如图,镜子中号码的实际号码是( )
 如图,镜子中号码的实际号码是( )
如图,镜子中号码的实际号码是( )| A. | 2653 | B. | 3562 | C. | 3265 | D. | 5623 |
1.已知二次函数y=x2-5x+m(m为实数)的图象与x轴上的一个交点为(2,0),则关于x的一元二次方程x2-5x+m=0的两实数根是( )
| A. | x1=2,x2=-2 | B. | x1=2,x2=3 | C. | x1=2,x2=0 | D. | x1=2,x2=-3 |
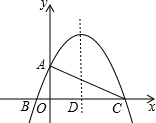 如图,已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC.
如图,已知二次函数y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4的图象与y轴交于点A,与x轴交于B、C两点,其对称轴与x轴交于点D,连接AC. 如图,△ABC与△A′B′C′关于直线l对称,若∠A=50°,∠C′=25°,则∠B的度数为105°.
如图,△ABC与△A′B′C′关于直线l对称,若∠A=50°,∠C′=25°,则∠B的度数为105°.