题目内容
15.线段AB长10cm,点P在线段AB上,且满足$\frac{BP}{AP}$=$\frac{AP}{AB}$,那么AP的长为5$\sqrt{5}$-5cm.分析 设AP=x,根据线段AB长10cm,得出BP=10-x,再根据$\frac{BP}{AP}$=$\frac{AP}{AB}$,求出x的值即可得出答案.
解答 解:设AP=x,则BP=10-x,
∵$\frac{BP}{AP}$=$\frac{AP}{AB}$,
∴$\frac{10-x}{x}$=$\frac{x}{10}$,
∴x1=5$\sqrt{5}$-5,x2=-5$\sqrt{5}$-5(不合题意,舍去),
∴AP的长为(5$\sqrt{5}$-5)cm.
故答案为:5$\sqrt{5}$-5.
点评 本题考查了黄金分割,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键.

练习册系列答案
相关题目
6.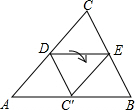 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
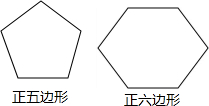 如图,小明用两根长度相等的铁丝,分别围成了正五边形和正六边形(正多边形的边长都相等),已知正五边形的边长比正六边形的边长多4cm.设正六边形的边长为xcm,根据题意,可列一元一次方程为5(x+4)=6x.
如图,小明用两根长度相等的铁丝,分别围成了正五边形和正六边形(正多边形的边长都相等),已知正五边形的边长比正六边形的边长多4cm.设正六边形的边长为xcm,根据题意,可列一元一次方程为5(x+4)=6x.
 如图所示,线段AB=2.8m,点C分AB为AC和BC的比为2:$\frac{4}{5}$,D为AB中点,求CD的长.
如图所示,线段AB=2.8m,点C分AB为AC和BC的比为2:$\frac{4}{5}$,D为AB中点,求CD的长.