题目内容
16.解下列方程:①x2-4x-6=0;
②3x(x+2)=5(x+2).
分析 ①先把方程的左边化为完全平方的形式,再利用直接开方法求出x的值即可;
②把方程化为两个因式积的形式,进而可得出结论.
解答 解:①原方程可化为x2-4x+4-4-6=0,即(x-2)2=10,
两边开方得,x-2=±$\sqrt{10}$,
故x1=2+$\sqrt{10}$,x2=2-$\sqrt{10}$;
②∵原方程可化为(x+2)(3x-5)=0,
∴x+2=0或3x-5=0,
∴x1=-2,x2=$\frac{5}{3}$.
点评 本题考查的是解一元二次方程,熟知因式分解法和配方法解一元二次方程是解答此题的关键.

练习册系列答案
相关题目
8.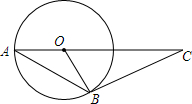 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )| A. | 65° | B. | 50° | C. | 40° | D. | 25° |
6.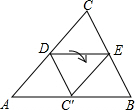 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
 如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将△CDE沿DE折叠,使点C落在AB边上的点C′处,若∠CDE=35°,则∠AC′D等于( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |

 一只蜘蛛正处于一个正方体的一个顶点A处,一只苍蝇处于此正方体的另一个顶点B处(如图所示),如果此正方体的棱长恰为10cm,试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm.
一只蜘蛛正处于一个正方体的一个顶点A处,一只苍蝇处于此正方体的另一个顶点B处(如图所示),如果此正方体的棱长恰为10cm,试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm.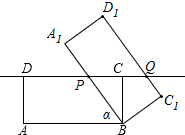 已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α<8)得到矩形A1B1C1D1.这两边所在的直线分别与CD边所在的直线相交于点P,Q,当DP:DQ=1:2时,DP的长为5.
已知矩形ABCD,AB=8,BC=4,将它绕着点B按顺时针方向旋转α度(0<α<8)得到矩形A1B1C1D1.这两边所在的直线分别与CD边所在的直线相交于点P,Q,当DP:DQ=1:2时,DP的长为5.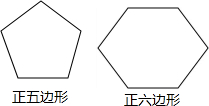 如图,小明用两根长度相等的铁丝,分别围成了正五边形和正六边形(正多边形的边长都相等),已知正五边形的边长比正六边形的边长多4cm.设正六边形的边长为xcm,根据题意,可列一元一次方程为5(x+4)=6x.
如图,小明用两根长度相等的铁丝,分别围成了正五边形和正六边形(正多边形的边长都相等),已知正五边形的边长比正六边形的边长多4cm.设正六边形的边长为xcm,根据题意,可列一元一次方程为5(x+4)=6x.