题目内容
13．在平面直角坐标系xOy中，有一个边长为2个单位长度的等边△ABC，满足AC∥y轴．平移△ABC得到△A′B′C′，使点A′、B′分别在x轴、y轴上（不包括原点），则此时点C′的坐标是（$\sqrt{3}$，2）或（$\sqrt{3}$，-2）或（-$\sqrt{3}$，2）或（-$\sqrt{3}$，-2）．分析 分两种情况：①B在AC左边；②B在AC右边；进行讨论，根据等边三角形的性质即可得到点C′的坐标．
解答 解：①如图1，B在AC左边；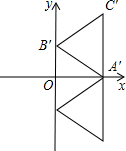
C′在第一象限，点C′的坐标是（$\sqrt{3}$，2）；
C′在第四象限，点C′的坐标是（$\sqrt{3}$，-2）；
②B在AC右边；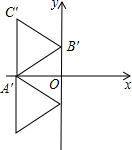
C′在第二象限，点C′的坐标是（-$\sqrt{3}$，2）；
C′在第三象限，点C′的坐标是（-$\sqrt{3}$，-2）．
故点C′的坐标是（$\sqrt{3}$，2）或（$\sqrt{3}$，-2）或（-$\sqrt{3}$，2）或（-$\sqrt{3}$，-2）．
故答案为：（$\sqrt{3}$，2）或（$\sqrt{3}$，-2）或（-$\sqrt{3}$，2）或（-$\sqrt{3}$，-2）．
点评 考查了坐标与图形变化-平移，解题关键是熟练掌握等边三角形的性质，以及分类思想的运用．
练习册系列答案
相关题目
4．下列式中能用平方差公式计算的有（ ）
①（x-$\frac{1}{2}$y）（x+$\frac{1}{2}$y）；②（3a-bc）（-bc-3a）；③（3-x+y）（3+x+y）；④（100+1）（100-1）
①（x-$\frac{1}{2}$y）（x+$\frac{1}{2}$y）；②（3a-bc）（-bc-3a）；③（3-x+y）（3+x+y）；④（100+1）（100-1）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
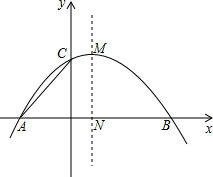如图，在平面直角坐标系中，抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴相交于A、B两点（点A位于点B的左侧），与y轴相交于点C，顶点M，对称轴MN与x轴相交于点N，连接AC．
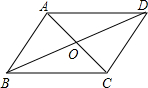如图，在?ABCD中，对角线AC，BD相交于点O，若BD与AC的和为18cm，CD：DA=2：3，△AOB的周长为13cm，求BC的长．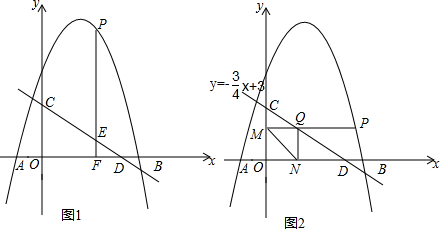
如图，在正方形ABCD中，E，F分别是AD、DC的中点，AF、BE交于点G，连接CG，试说明：△CGB是等腰三角形．
3．近视眼镜的度数y（度）与镜片焦距x（m）成反比例，已知200度近视眼镜镜片的焦距为0.5m，则y与x的函数关系式为（ ）
| A． | y=$\frac{100}{x}$ | B． | y=$\frac{1}{2x}$ | C． | y=$\frac{200}{x}$ | D． | y=$\frac{1}{200x}$ |