题目内容
8.观察下列式子,并探索它们的规律:$\frac{1}{1×2}$=1-$\frac{1}{2}$,
$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,
$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,
…
试用正整数n表示这个规律,并加以证明.
分析 分母是两个连续自然数的乘积,分子是1的分数可以拆成这两个自然数为分母,分子是1的两个分数的差,由此规律得出答案即可.
解答 解:∵$\frac{1}{1×2}$=1-$\frac{1}{2}$,
$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,
$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,
…
∴$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
证明:∵$\frac{1}{n}$-$\frac{1}{n+1}$.
=$\frac{n+1}{n(n+1)}$-$\frac{n}{n(n+1)}$
=$\frac{1}{n(n+1)}$,
∴$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
19.下列说法错误的是( )
| A. | 整数与分数统称为有理数 | B. | 最小的正整数是0 | ||
| C. | 负整数,0与正整数统称为整数 | D. | 互为相反数的两个数的和等于0 |
3.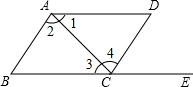 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠3 | B. | ∠D=∠DCE | C. | ∠2=∠4 | D. | ∠D+∠BCD=180° |
18.小红在报纸上看到淡水资源的一份报道,世界人均可再生淡水资源6521立方米,中国人均可再生淡水资源仅2134立方米,淡水消费分三类:农业用水、工业用水、生活用水,三类淡水消费所占百分比如图所示:

图中只有世界淡水消费中农业用水的百分比为82.5%,其余百分比都看不清了,但报纸中说到在淡水消费中:中国工业用水所占百分比是世界工业用水所占百分比的3倍还多3.8个百分点,中国农业用水所占百分比比中国工业用水所占百分比多42个百分点,中国生活用水所占百分比比世界生活用水所占百分比少3.6个百分点.请利用列二元一次方程组计算出三类淡水消费其余各项百分比,写出完整的解答题并填写到统计表中.

图中只有世界淡水消费中农业用水的百分比为82.5%,其余百分比都看不清了,但报纸中说到在淡水消费中:中国工业用水所占百分比是世界工业用水所占百分比的3倍还多3.8个百分点,中国农业用水所占百分比比中国工业用水所占百分比多42个百分点,中国生活用水所占百分比比世界生活用水所占百分比少3.6个百分点.请利用列二元一次方程组计算出三类淡水消费其余各项百分比,写出完整的解答题并填写到统计表中.
| 三类淡水消费所占百分比 | |||
| 农业用水 | 工业用水 | 生活用水 | |
| 世界 | 82.5% | 7.3% | 10.2% |
| 中国 | 67.7% | 25.7% | 6.6% |
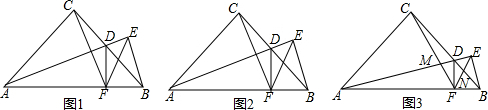
 如图是一束平行光线从教室窗户射入的平面示意图,BC=1,NC=$\frac{4}{3}$,BN=$\frac{5}{3}$,AB=3.5,MN=$\frac{14}{3}$,求AM的长度.
如图是一束平行光线从教室窗户射入的平面示意图,BC=1,NC=$\frac{4}{3}$,BN=$\frac{5}{3}$,AB=3.5,MN=$\frac{14}{3}$,求AM的长度.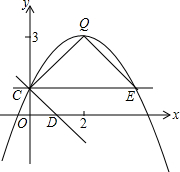 如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC
如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC