题目内容
1.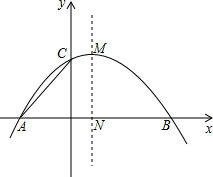 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴相交于A、B两点(点A位于点B的左侧),与y轴相交于点C,顶点M,对称轴MN与x轴相交于点N,连接AC.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2与x轴相交于A、B两点(点A位于点B的左侧),与y轴相交于点C,顶点M,对称轴MN与x轴相交于点N,连接AC.(1)求A、B两点的坐标;
(2)求∠CAO的大小;
(3)抛物线的对称轴MN上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
分析 (1)令y=0求得x的值即可求得与x轴的交点坐标;
(2)求得点C的坐标后即可得到AO=CO,从而得到∠CAO的度数;
(3)首先求得直线AC的解析式,然后设垂直于AC的解析式为y=-x+b,然后分当经过点C与AC垂直和经过点A且垂直于AC两种情况求得结果即可.
解答 解:(1)令y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2=0,
解得:x=-2或x=4,
故A点的坐标为(-2,0),点B的坐标为(4,0);
(2)∵令x=0,则y=2,
∴点C的坐标为(0,2),
∴AO=CO=2,
∴∠CAO=45°;
(3)∵抛物线y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2=-$\frac{1}{4}$(x-1)2+$\frac{9}{4}$,
∴对称轴为x=1,
∵A(-2,0),C(0,2),
∴直线AC的解析式为y=x+2,
当直角△ACP的直角边PC经过点C时,
设直线PC的解析式为y=-x+b,
∵经过点C(0,2),
∴直线PC的解析式为y=-x+2,
∴当x=1时,y=-1+2=1,
∴点P的坐标为(1,1);
当直角△ACP的直角边PA经过点A时,
设直线PA的解析式为y=-x+b,
∵经过点A(-2,0),
∴直线AP的解析式为y=-x-2,
∴当x=1时,y=-1-2=-3,
∴点P的坐标为(1,-3);
综上所述:点P的坐标为(1,1)和(1,-3).
点评 本题考查了二次函数的综合知识,重点考查了与坐标轴的交点坐标及待定系数法的知识,特别是第(3)题中的分类讨论数学思想更是中考的热点考题之一,难度中等.

练习册系列答案
相关题目
 如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数.
如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数. 如图,AD是△ABC边BC上的高,CD=5,BD=3,cos∠BAD=tan∠ACD.
如图,AD是△ABC边BC上的高,CD=5,BD=3,cos∠BAD=tan∠ACD.
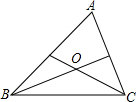 三角形的三条角平分线的交点叫做三角形的内心.如图,点O是△ABC的内心,若∠A=80°,则∠BOC=130°.
三角形的三条角平分线的交点叫做三角形的内心.如图,点O是△ABC的内心,若∠A=80°,则∠BOC=130°.