题目内容
10. 如图,抛物线y=-$\frac{5}{4}$x2+$\frac{17}{4}$x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)
如图,抛物线y=-$\frac{5}{4}$x2+$\frac{17}{4}$x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0)(1)求直线AB的函数关系式;
(2)动点P在线段OC上从原点出发以每秒一个单位的速度向C移动.过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长度为s个单位,求s与t的函数关系式,并写出t的取值范围;
(3)当线段MN最长时,求出△ABN的面积;
(4)设在(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM、BN.当t为何值时,四边形BCMN为平行四边形?问对于所求的t值,平行四边形BCMN是否菱形?请说明理由.
分析 (1)根据函数图象上点的坐标特征求出点A、点B的坐标,利用待定系数法求出直线AB的函数关系式;
(2)分别求出点M和点N的纵坐标,得到s与t的函数关系式;
(3)根据二次函数的性质求出MN的最大值,根据三角形的面积公式计算即可;
(4)根据平行四边形的判定和菱形的判定定理解答.
解答 解:(1)x=0时,y=1,
∴点A的坐标为:(0,1),
∵BC⊥x轴,垂足为点C(3,0),
∴点B的横坐标为3,
当x=3时,y=$\frac{5}{2}$,
∴点B的坐标为(3,$\frac{5}{2}$),
设直线AB的函数关系式为y=kx+b,
$\left\{\begin{array}{l}{b=1}\\{3k+b=\frac{5}{2}}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
则直线AB的函数关系式y=$\frac{1}{2}$x+1;
(2)当x=t时,y=$\frac{1}{2}$t+1,
∴点M的坐标为(t,$\frac{1}{2}$t+1),
当x=t时,y=-$\frac{5}{4}$t2+$\frac{17}{4}$t+1,
∴点N的坐标为(t,-$\frac{5}{4}$t2+$\frac{17}{4}$t+1),
s=-$\frac{5}{4}$t2+$\frac{17}{4}$t+1-($\frac{1}{2}$t+1)=-$\frac{5}{4}$t2+$\frac{15}{4}$t(0≤t≤3);
(3)s=-$\frac{5}{4}$t2+$\frac{15}{4}$t=-$\frac{5}{4}$(t-$\frac{3}{2}$)2+$\frac{45}{16}$,
当x=$\frac{3}{2}$时,MN有最大值$\frac{45}{16}$,
△ABN的面积=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{45}{16}$+$\frac{1}{2}$×$\frac{3}{2}$×$\frac{45}{16}$=$\frac{135}{32}$;
(4)若四边形BCMN为平行四边形,则有MN=BC,
∴-$\frac{5}{4}$t2+$\frac{15}{4}$t=$\frac{5}{2}$,
解得t1=1,t2=2,
∴当t=1或2时,四边形BCMN为平行四边形,
①当t=1时,MP=$\frac{3}{2}$,PC=2,
∴MC=$\frac{5}{2}$=MN,此时四边形BCMN为菱形,
②当t=2时,MP=2,PC=1,
∴MC=$\sqrt{5}$≠MN,此时四边形BCMN不是菱形.
点评 本题考查的是二次函数的性质、待定系数法求函数解析式、菱形的判定,正确求出二次函数的解析式、利用配方法把一般式化为顶点式、求出函数的最值是解题的关键,注意菱形的判定定理的灵活运用.

| 年龄(岁) | 11 | 12 | 13 | 14 | 15 |
| 人数 | 3 | 3 | 7 | 12 | 14 |
| 体重(千克) | 频数 | 频率 |
| 40-45 | 44 | |
| 45-50 | 66 | |
| 50-55 | 84 | |
| 55-60 | 86 | |
| 60-65 | 72 | |
| 65-70 | 48 |
| A. | a>0 | B. | a>2 | C. | 1<a<3 | D. | a>3 |
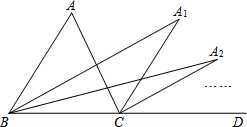 如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.
如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…∠An-1BC的平行线与∠An-1CD的平分线交于点An,设∠A=θ,则∠An=$\frac{θ}{{2}^{n}}$.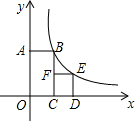 如图,四边形OABC是矩形,四边形CDEF是正方形,点C,D在x轴的正半轴上,点A在y轴的正半轴上,点F在BC上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=1,则正方形CDEF的面积为( )
如图,四边形OABC是矩形,四边形CDEF是正方形,点C,D在x轴的正半轴上,点A在y轴的正半轴上,点F在BC上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=1,则正方形CDEF的面积为( )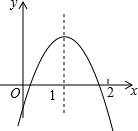 二次函数y=ax2+bx+c的图象如图所示,下列结论:
二次函数y=ax2+bx+c的图象如图所示,下列结论: