题目内容
7.(1)分解因式:4a(a-1)2-(1-a)(2)解方程:2x2+4x-1=0
(3)解不等式组$\left\{\begin{array}{l}{x+\frac{1}{2}>2x-1}\\{\frac{x+1}{2}≤\frac{1+2x}{3}+1}\end{array}\right.$,并求出它的所有整数解.
分析 (1)利用提公因式法分解,然后利用公式法即可分解;
(2)利用求根公式即可求解;
(3)先求出不等式组中每一个不等式的解集,再求出它们的公共部分就是不等式组的解集,然后确定整数解即可.
解答 解:(1)原式=4a(a-1)2+(a-1)=(a-1)【4a(a-1)+1】=(a-1)(4a2-4a+1)=(a-1)(2a-1)2;
(2)∵a=2,b=4,c=-1,
b2-4ac=16+8=24>0,
∴x=$\frac{-4±\sqrt{24}}{4}$,
则x1=$\frac{-2+\sqrt{6}}{2}$,x2=$\frac{-2-\sqrt{6}}{2}$;
(3)$\left\{\begin{array}{l}{x+\frac{1}{2}>2x-1…①}\\{\frac{x+1}{2}≤\frac{1+2x}{3}+1…②}\end{array}\right.$,
解①得x<$\frac{3}{2}$,
解②得:x≥-5.
则不等式组的解集是-5≤x<$\frac{3}{2}$.
则整数解是:-5,-4,-3,-2,-1,0,1.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.要注意x是否取得到,若取得到则x在该点是实心的.反之x在该点是空心的.

练习册系列答案
相关题目
18.若分式$\frac{|x|-1}{x+1}$的值为0,则( )
| A. | x=±1 | B. | x=1 | C. | x=-1 | D. | x=0 |
2.下列调查中,适合普查的是( )
| A. | 了解某文稿的错别字情况 | B. | 了解某种灯泡的使用寿命情况 | ||
| C. | 了解某市学生的视力情况 | D. | 了解某市老年人参加晨练的情况. |
12.若代数式x(x-5)与5(5-x)的值相等,则x的值是( )
| A. | 5 | B. | -5 | C. | ±5 | D. | 5或0 |
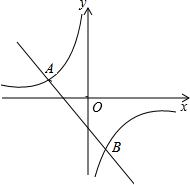 如图,一次函数y1的图象与反比例函数y2的图象交于A(-5,2)、B(m,-5)两点.
如图,一次函数y1的图象与反比例函数y2的图象交于A(-5,2)、B(m,-5)两点.