题目内容
17.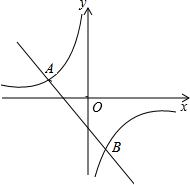 如图,一次函数y1的图象与反比例函数y2的图象交于A(-5,2)、B(m,-5)两点.
如图,一次函数y1的图象与反比例函数y2的图象交于A(-5,2)、B(m,-5)两点.(1)求的函数y1、y2表达式;
(2)观察图象,当时-4<x<2,比较y1、y2的大小?
分析 (1)设一次函数y1的解析式为y1=k1x+b,反比例函数的解析式为y2=$\frac{{k}_{2}}{x}$,将点A的坐标代入反比例函数的解析式可得k2=-10,进而求得:m=2.即A(-5,2),B(2,-5)在直线y1=k1x+b上,将其坐标代入即求可得一次函数的解析式.
(2)根据图象,易得y1与y2的大小关系.
解答 解:(1)设一次函数y1的解析式为y1=k1x+b,反比例函数的解析式为y2=$\frac{{k}_{2}}{x}$,
∵点A(-5,2)在双曲线y2=$\frac{{k}_{2}}{x}$上,
∴k2=-10.
∴反比例函数的解析式为:y2=-$\frac{10}{x}$.
∵B(m,-5)在双曲线y2=-$\frac{10}{x}$上,
∴m=2.
∴B(2,-5).
∵A(-5,2)B(2,-5)在直线y1=k1x+b上,
∴$\left\{\begin{array}{l}{2=-5{k}_{1}+b}\\{-5=2{k}_{1}+b}\end{array}\right.$,
解之得 $\left\{\begin{array}{l}{{k}_{1}=-1}\\{b=-3}\end{array}\right.$,
一次函数的解析式为:y1=-x-3.
(2)由图象可得:
当-4<x<0时,y1<y2;
当0<x<2时,y1>y2.
点评 本题考查反比例函数与一次函数的解得问题,熟练掌握待定系数法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列说法
①点到直线的距离是点到直线所作的垂线; ②算术平方根等于它本身的数只有1和0;
③两个角相等,这两个角是对顶角; ④过一点有且只有一条直线与已知直线平行.
其中正确的有( )
①点到直线的距离是点到直线所作的垂线; ②算术平方根等于它本身的数只有1和0;
③两个角相等,这两个角是对顶角; ④过一点有且只有一条直线与已知直线平行.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.七(1)班学雷锋小组整理校实验室,已知6个人共要做4小时完成,则每人每小时的工作效率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{24}$ |
9.如果三角形ABC中,∠A:∠B:∠C=1:1:2,那么BC:AC:AB的值为( )
| A. | 1:1:2 | B. | 1:2:1 | C. | 2:1:1 | D. | 1:1:$\sqrt{2}$ |
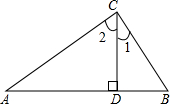 如图,在△ABC中,CD⊥AB于D,若a、b、c是三角形的三条边长,c边上的高CD的长是h,下列条件中一定能确定△ABC为直角三角形的是①②④.(只要填写正确的序号)
如图,在△ABC中,CD⊥AB于D,若a、b、c是三角形的三条边长,c边上的高CD的长是h,下列条件中一定能确定△ABC为直角三角形的是①②④.(只要填写正确的序号)