题目内容
17.△ABC与△A′B′C′中,条件①AB=A′B′,②BC=B′C′,③AC=A′C′,④∠A=∠A′,⑤∠B=∠B′,⑥∠C=∠C′,则下列各组条件中不能保证△ABC≌△A′B′C′的是( )| A. | ①②③ | B. | ①③⑤ | C. | ①②⑤ | D. | ②⑤⑥ |
分析 根据全等三角形的判定方法对各选项分别进行判断.
解答 解:A、由①②③,可根据“SSS”判定△ABC≌△A′B′C′;
B、由①③⑤不能判定△ABC≌△A′B′C′;
C、由①②⑤,可根据“SAS”判定△ABC≌△A′B′C′;
D、由②⑤⑥,可根据“ASA”判定△ABC≌△A′B′C′.
故选B.
点评 本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
相关题目
12.a=5+2$\sqrt{6}$,b=$\frac{{\sqrt{3}+\sqrt{2}}}{{\sqrt{3}-\sqrt{2}}}$,则a与b的关系是( )
| A. | a=b | B. | ab=1 | C. | a>b | D. | a<b. |
6. 记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
 记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )
记抛物线y=-x2+2013的图象与y轴正半轴的交点为A,将线段OA分成2013等份,设分点分别为P1,P2…P2012,过每个分点作y轴的垂线,分别与抛物线交于点Q1,Q2,…Q2012,再记直角三角形OP1Q1,P1P2Q2…的面积分别为S1,S2,…,这样就记W=S${\;}_{1}^{2}$+S${\;}_{2}^{2}$+…+S${\;}_{2012}^{2}$,W的值为( )| A. | $\frac{2013×2012}{4}$ | B. | $\frac{2013×2012}{2}$ | C. | $\frac{503×2013}{2}$ | D. | $\frac{2012×2011}{4}$ |
7.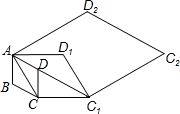 如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
 如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )
如图,边长为1的菱形ABCD,∠DAB=60°,则菱形ABCD的面积是$\frac{\sqrt{3}}{2}$;连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°,则菱形ACC1D1的面积是$\frac{3\sqrt{3}}{2}$;连接对角线AC1,再以AC1为边作第三个菱形AC1C2D,使∠D2AC1=60°,则菱形AC1C2的面积是$\frac{9\sqrt{3}}{2}$;…;按此规律所作的第n个菱形的面积为( )| A. | $\frac{\sqrt{3}}{2}$×3n | B. | $\frac{\sqrt{3}}{2}$×3n+1 | C. | $\frac{\sqrt{3}}{2}$×3n-1 | D. | $\frac{\sqrt{3}}{2}$×32n-1 |
 如图,已知:A、F、C、D四点在一条直线上,AF=CD,BC=EF,且AB=DE. 请说明△ABC≌△DEF.
如图,已知:A、F、C、D四点在一条直线上,AF=CD,BC=EF,且AB=DE. 请说明△ABC≌△DEF.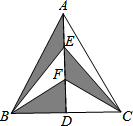 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的三等分点,若△ABC的面积为12cm2,则图中的阴影面积是6cm2.