题目内容
15.抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点,(1)求出这个抛物线并画出这条抛物线;
(2)求它与x轴的交点和抛物线顶点的坐标;
(3)x取什么值时,抛物线在x轴上方?
(4)x取什么值时,y的值随x的增大而减小?
分析 由已知点(0,3)代入y=-x2+(m-1)x+m即可求得m的值,即可知道二次函数解析式,并可画出图象,然后根据图象和二次函数性质可得(2)(3)(4).
解答 解:(1)由题意将(0,3)代入解析式可得m=3,
∴抛物线为y=-x2+2x+3.
(2)令y=0,则-x2+2x+3=0,得x1=-1,x2=3;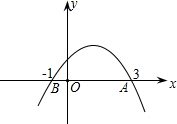
∴抛物线与x轴的交点为(-1,0),(3,0).
∵y=-x2+2x+3=-(x-1)2+4,
∴抛物线顶点坐标为(1,4);
(3)由图象可知:当-1<x<3时,抛物线在x轴上方;
(4)由图象可知:当x>1时,y的值随x值的增大而减小.
点评 本题考查了抛物线与x轴的交点.掌握坐标轴上的点的坐标特征和二次函数图象上点的坐标特征是解题的关键.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
10.下面的计算正确的是( )
| A. | a+2a=3a2 | B. | a3÷a=3 | C. | a2•a3=a5 | D. | -(a)3=a3 |
4.方程x2-7x+12=0的解为( )
| A. | 3或4 | B. | -3或-4 | C. | -3或4 | D. | 3或-4 |
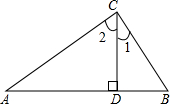 如图,在△ABC中,CD⊥AB于D,若a、b、c是三角形的三条边长,c边上的高CD的长是h,下列条件中一定能确定△ABC为直角三角形的是①②④.(只要填写正确的序号)
如图,在△ABC中,CD⊥AB于D,若a、b、c是三角形的三条边长,c边上的高CD的长是h,下列条件中一定能确定△ABC为直角三角形的是①②④.(只要填写正确的序号)