题目内容
9.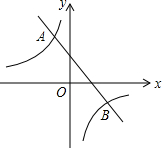 如图,在同一平面直角坐标系中,直线y1=ax+b与双曲线y2=$\frac{k}{x}$相交于点A(-1,3)和点B(3,-1),则当y1<y2时,x的取值范围是-1<x<0或x>3.
如图,在同一平面直角坐标系中,直线y1=ax+b与双曲线y2=$\frac{k}{x}$相交于点A(-1,3)和点B(3,-1),则当y1<y2时,x的取值范围是-1<x<0或x>3.
分析 根据图象知,两个函数的图象的交点是(-1,3),(3,-1).由图象可以直接写出当y1<y2时所对应的x的取值范围.
解答 解:根据图象知,一次函数y1=kx+b与反比例函数y2=$\frac{k}{x}$的交点是(-1,3),(3,-1),
∴当y1<y2时,-1<x<0或x>3;
故答案为:-1<x<0或x>3.
点评 本题主要考查了反比例函数与一次函数的交点问题.解答此题时,采用了“数形结合”的数学思想.

练习册系列答案
相关题目
4.将平行四边形的四边中点顺次连接而形成的新的四边形是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
14.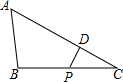 如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
 如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )
如图,在△ABC中,∠ABC>90°,∠C=30°,BC=12,P是BC上的一个动点,过点P作PD⊥AC于点D,设CP=x,△CDP的面积为y,则y与x之间的函数图象大致为( )| A. | 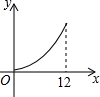 | B. | 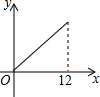 | C. | 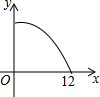 | D. | 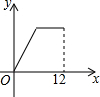 |

 如图,在等腰△ABC中,腰长AB=AC=8厘米,底边BC=6厘米,点D为AB的中点.如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动.当点N的运动速度为2或$\frac{8}{3}$厘米/秒时,能够使△BMD与△CNM全等.
如图,在等腰△ABC中,腰长AB=AC=8厘米,底边BC=6厘米,点D为AB的中点.如果点M在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点N在线段CA上由C点向A点运动.当点N的运动速度为2或$\frac{8}{3}$厘米/秒时,能够使△BMD与△CNM全等. 某商店经销甲、乙两种商品.请您根据图中所给的信息解答下列问题:
某商店经销甲、乙两种商品.请您根据图中所给的信息解答下列问题: