题目内容
4.将平行四边形的四边中点顺次连接而形成的新的四边形是( )| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
分析 根据题意和三角形中位线定理证明EF∥HG,EF=HG,根据平行四边形的判定定理证明结论.
解答 解∵E、F分别为AB、BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
∵G、H分别为CD、DA的中点,
∴HG∥AC,HG=$\frac{1}{2}$AC,
∴EF∥HG,EF=HG,
∴四边形EFGH为平行四边形.
故选:A.
点评 本题考查的是平行四边形的性质和判定以及三角形的中位线定理,正确运用三角形的中位线定理和平行四边形的判定定理是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
15.下列命题正确的是( )
| A. | 若两条弧的长相等,则这两条弧是等弧 | |
| B. | 两条弧的长相等,它们所对的圆心角也相等 | |
| C. | 两个相等的圆心角所对的两条弧的长相等 | |
| D. | 如果两个圆的周长相等,那么它们的半径也相等 |
16.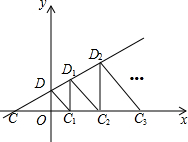 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
 如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )
如图,直线y=$\frac{1}{2}$x+1与x轴、y轴分别交于点C、D,以线段OD为直角边作等腰Rt△DOC1,过点C1作C1D1⊥x轴交直线y=$\frac{1}{2}$x+1于点D1,又以C1D1为直角边作等腰Rt△D1C1C2,…按这样规律一直作下去,则Rt△D2013C2013C2014的腰长是( )| A. | $\frac{4025}{2014}$ | B. | $\frac{{3}^{2012}}{{3}^{2013}}$ | C. | $\frac{{3}^{2013}}{{3}^{2012}}$ | D. | ($\frac{3}{2}$)2013 |
 如图,AB=AD,AC=AE,∠1=∠2,则下列正确结论有(1)(2)(4)(只填序号).
如图,AB=AD,AC=AE,∠1=∠2,则下列正确结论有(1)(2)(4)(只填序号).
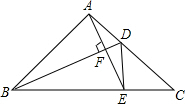 如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.
如图,在△ABC中,BD是角平分线,AB=AC=5,BC=8,过A作AE⊥BD交于F,交BC于E,连结DE,则S△ABF:S△CDE=$\frac{65}{48}$.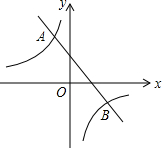 如图,在同一平面直角坐标系中,直线y1=ax+b与双曲线y2=$\frac{k}{x}$相交于点A(-1,3)和点B(3,-1),则当y1<y2时,x的取值范围是-1<x<0或x>3.
如图,在同一平面直角坐标系中,直线y1=ax+b与双曲线y2=$\frac{k}{x}$相交于点A(-1,3)和点B(3,-1),则当y1<y2时,x的取值范围是-1<x<0或x>3.



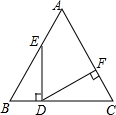 如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°.
如图,在等边△ABC中,点D为BC边上的点,DE⊥BC交AB于E,DF⊥AC于F,则∠EDF的度数为60°.