题目内容
19.如图1,BP、CP是△ABC中∠ABC、∠ACB的角平分线,∠A=50°,可知∠P=115°;如图2的四边形ABCD,BP、CP仍然是∠ABC、∠BCD的角平分线,猜想∠BPC与∠A,∠D有何数量关系∠BPC=$\frac{1}{2}$∠BAD+$\frac{1}{2}$∠ADC.
分析 根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解;
延长BA、CD相交于点E.根据已知的结论,得∠BPC=90°+$\frac{1}{2}$∠BEC.结合三角形的外角的性质,得∠E=∠BAD-∠ADE=∠BAD-(180°-∠ADC),再进一步代入化简即可.
解答 解:∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵∠ABC与∠ACB的角平分线相交于P,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×130°=65°,
在△PBC中,∠BPC=180°-(∠PBC+∠PCB)=180°-65°=115°.
如图2,延长BA、CD相交于点E.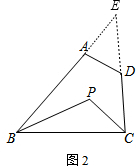
根据已知的结论,得∠BPC=90°+$\frac{1}{2}$∠BEC.
又∠E=∠BAD-∠ADE=∠BAD-(180°-∠ADC).
∴∠BPC=90°+$\frac{1}{2}$∠BAD-90°+$\frac{1}{2}$∠ADC.
即∠BPC=$\frac{1}{2}$∠BAD+$\frac{1}{2}$∠ADC.
故答案为:115°,∠BPC=$\frac{1}{2}$∠BAD+$\frac{1}{2}$∠ADC.
点评 本题考查了多边形的内角与外角,解决此题的时候,注意构造三角形,直接运用已知的结论,再进一步利用三角形的外角的性质进行转换.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
4.为了满足学生的物质需求,重庆市某重点中学到mama超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该mama超市有几种进货方案?
(3)在(2)的条件下,该mama超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠a(2<a<7)元出售,乙种袋装食品价格不变.那么该mama超市要获得最大利润应如何进货?
| 甲 | 乙 | |
| 进价(元/袋) | m | m-2 |
| 售价(元/袋) | 20 | 13 |
(1)求m的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该mama超市有几种进货方案?
(3)在(2)的条件下,该mama超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠a(2<a<7)元出售,乙种袋装食品价格不变.那么该mama超市要获得最大利润应如何进货?
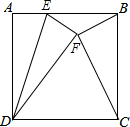 如图,已知E是正方形ABCD的边AB上一点,点A关于DE的对称点为F,∠BFC=90°,求$\frac{AB}{AE}$的值.
如图,已知E是正方形ABCD的边AB上一点,点A关于DE的对称点为F,∠BFC=90°,求$\frac{AB}{AE}$的值. 如图,AB=AD,AC=AE,∠1=∠2,则下列正确结论有(1)(2)(4)(只填序号).
如图,AB=AD,AC=AE,∠1=∠2,则下列正确结论有(1)(2)(4)(只填序号).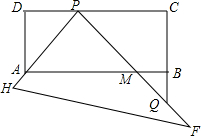 如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm.
如图,有一块塑料矩形模板ABCD,AB=5cm,AD=2cm,将足够大的直角三角形PHF的直角顶点P落在CD边上(不与C、D重合),在CD上适当移动三角板顶点P,使直角边PH始终通过点A,另一直角边PF与CB的延长线交于点Q,与AB交于点M.若BM=1cm,则DP=2 cm.
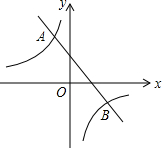 如图,在同一平面直角坐标系中,直线y1=ax+b与双曲线y2=$\frac{k}{x}$相交于点A(-1,3)和点B(3,-1),则当y1<y2时,x的取值范围是-1<x<0或x>3.
如图,在同一平面直角坐标系中,直线y1=ax+b与双曲线y2=$\frac{k}{x}$相交于点A(-1,3)和点B(3,-1),则当y1<y2时,x的取值范围是-1<x<0或x>3.