题目内容
5.某商店对一种名牌衬衫抽测结果如下表:| 抽检件数 | 10 | 20 | 100 | 150 | 200 | 300 |
| 不合格件数 | 0 | 1 | 3 | 4 | 6 | 9 |
分析 先利用频率估计概率的思想,求出从这批衬衣中任抽1件是次品的概率,再根据需要准备顾客更换的合格品衬衫数=销售的衬衫数×次品的概率,即可求解.
解答 解:抽查总体数:10+20+100+150+200+300=780,
次品件数:0+1+3+4+6+9=23,
P(抽到次品)=$\frac{23}{780}$≈0.03.
则1000×0.03=30(件).
答:至少要多准备30件合格品,以便供顾客更换.
故答案为:30.
点评 本题考查了利用频率估计概率及概率的计算,是统计在实际生活中应用,问题的生活化可激发学生的兴趣和求知欲望,同样这样的问题也影响学生的思维方式,学会用数学的视野关注身边的数学.

练习册系列答案
相关题目
15.若$\frac{1}{2}{x^{a-1}}{y^{2b}}$与$-\frac{1}{3}{x^{2-b}}{y^2}$是同类项,则a、b值分别为( )
| A. | a=2,b=-1 | B. | a=2,b=1 | C. | a=-2,b=1 | D. | a=-2,b=-1 |
20.将抛物线y=4x2先沿x轴方向向左平移2个单位,再沿y轴方向向下平移3个单位,所得抛物线的解析式是( )
| A. | y=4(x+2)2-3 | B. | y=4(x-2)2-3 | C. | y=4(x+2)2+3 | D. | y=4(x+3)2+2 |
17.方程x$\sqrt{2-x}$=$\sqrt{2-x}$的解是( )
| A. | x1=2,x1=1,x3=-1 | B. | x1=2,x2=1 | C. | x1=2,x2=-1 | D. | x1=1,x2=-1 |
14.已知⊙O1与⊙O2的半径分别为3cm和4cm,两元的圆心距为7cm,则两圆的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内含 |
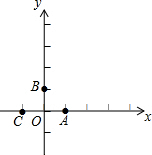 如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2015的坐标为(-2,0).
如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P2015的坐标为(-2,0).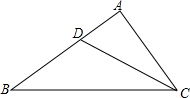 如图,△ABC中,已知∠A=2∠B,CD是∠ACB的平分线,试说明BC=AD+AC.(提示:在BC边上取点E,使EC=AC,联结DE).
如图,△ABC中,已知∠A=2∠B,CD是∠ACB的平分线,试说明BC=AD+AC.(提示:在BC边上取点E,使EC=AC,联结DE).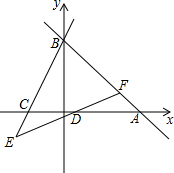 如图,直线y=-x+6与x轴交于点A,与y轴交于点B,C(-2,0),直线y=kx-k与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF,求k的值.
如图,直线y=-x+6与x轴交于点A,与y轴交于点B,C(-2,0),直线y=kx-k与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF,求k的值.