题目内容
2.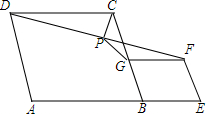 如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG、PC.若∠ABC=60°,AB=3,BE=1,则PG的长度=$\sqrt{3}$.
如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG、PC.若∠ABC=60°,AB=3,BE=1,则PG的长度=$\sqrt{3}$.
分析 延长GP交CD于H,由菱形的性质得出CD∥AB∥GF,BC=CD=AB=3,BG=GF=BE=1,由ASA证明△PGF≌△PHD,得出对应边相等PH=PG,DH=FG,得出CH=CG,再根据等腰三角形三线合一的性质得出∠PCG=$\frac{1}{2}$×120°=60°,得出∠PGC=30°,求出PC,得出PG即可.
解答 解:延长GP交CD于H,如图所示: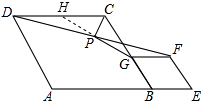 ∵四边形ABCD和四边形BEFG是菱形,
∵四边形ABCD和四边形BEFG是菱形,
∴CD∥AB∥GF,BC=CD=AB=3,BG=GF=BE=1,
∴∠PDH=∠PFG,
∵P是线段DF的中点,
∴PD=PF,
在△PGF和△PHD中,
$\left\{\begin{array}{l}{∠PDH=∠PFG}&{\;}\\{PD=PF}&{\;}\\{∠DPH=∠FPG}&{\;}\end{array}\right.$,
∴△PGF≌△PHD(ASA),
∴PH=PG,DH=FG=1,
∵CH=CD-DH=3-1=2,CG=BC-BG=3-1=2,
∴CH=CG,
∴PG⊥PC,∠PCG=∠PCH,
∵∠ABC=∠BEF=60°,
∴∠BCD=180°-60°=120°,
∴∠PCG=$\frac{1}{2}$×120°=60°,
∴∠PGC=30°,
∴PC=$\frac{1}{2}$CG=1,
∴PG=$\sqrt{3}$PC=$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 本题主要考查了菱形的性质、全等三角形的判定与性质、等腰三角形三线合一的性质、含30°角的直角三角形的性质、三角函数等知识;本题综合性强,有一定难度,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
 已知数轴上两点A,B对应的数分别为-1,3,P为数轴上的动点,其对应的数为x.
已知数轴上两点A,B对应的数分别为-1,3,P为数轴上的动点,其对应的数为x.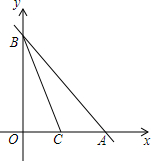 如图,在平面直角坐标系中,直线y=-x+4与坐标轴分别交A,B两点,点C(2,0),连接BC,点P为线段AB上一动点,连接OP,OP交BC于点D
如图,在平面直角坐标系中,直线y=-x+4与坐标轴分别交A,B两点,点C(2,0),连接BC,点P为线段AB上一动点,连接OP,OP交BC于点D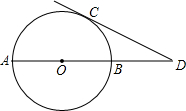 如图,AB是⊙O的直径,过点C的切线交AB的延长线于点D.若∠ADC=30°,BD=10,求⊙O的半径.
如图,AB是⊙O的直径,过点C的切线交AB的延长线于点D.若∠ADC=30°,BD=10,求⊙O的半径.