题目内容
13.若(2x-1)2+|3y+2|=0,则x=$\frac{1}{2}$,y=-$\frac{2}{3}$.分析 根据非负数的和为零,可得每个非负数同时为零;根据解方程,可得答案.
解答 解:由(2x-1)2+|3y+2|=0,得
2x-1=0,3y+2=0,
解得x=$\frac{1}{2}$,y=-$\frac{2}{3}$,
故答案为:$\frac{1}{2}$,-$\frac{2}{3}$.
点评 本题考查了非负数的性质,利用非负数的和为零得出每个非负数同时为零是解题关键.

练习册系列答案
相关题目
4.下列判断中,正确的是( )
| A. | x的系数是0 | B. | y的次数是0 | ||
| C. | 23xyz是三次单项式 | D. | 24与42不是同类项 |
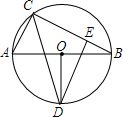 已知:如图,在⊙O中,AB是直径,OD⊥AB,连接CD,过D作DE垂直于BC于E,AB=8,CD=6,求BE的长.
已知:如图,在⊙O中,AB是直径,OD⊥AB,连接CD,过D作DE垂直于BC于E,AB=8,CD=6,求BE的长.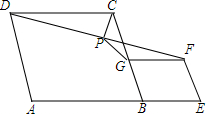 如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG、PC.若∠ABC=60°,AB=3,BE=1,则PG的长度=$\sqrt{3}$.
如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG、PC.若∠ABC=60°,AB=3,BE=1,则PG的长度=$\sqrt{3}$.